The position Vectors of two identical particles with respect to the origin in the three-dimensional coordinator system are r1andr2 The position of the centre of mass of the system is given by
r1+r2
2(r1+r2)
r1−r2
r1+r22
The correct Answer is:D
To find the position of the center of mass of two identical particles with position vectors r1 and r2, we can follow these steps:
1. Understanding the Problem: We have two identical particles, which means they have the same mass. Let's denote the mass of each particle as m. The position vectors of the particles with respect to the origin are given as r1 and r2.
2. Formula for Center of Mass: The formula for the center of mass RCM for a system of particles is given by:
RCM=1Mn∑i=1miri
where M is the total mass of the system, mi is the mass of each particle, and ri is the position vector of each particle.
3. Applying the Formula: For our case with two identical particles:
- The total mass M=m1+m2=m+m=2m.
- The position vectors are r1 and r2.
- Thus, the center of mass can be calculated as:
RCM=12m(mr1+mr2)
4. Simplifying the Expression: Since both particles have the same mass m, we can factor out m:
RCM=12mm(r1+r2)=r1+r22
5. Final Result: Therefore, the position of the center of mass of the system is:
RCM=r1+r22
RCM=1Mn∑i=1miri
where M is the total mass of the system, mi is the mass of each particle, and ri is the position vector of each particle.
- The total mass M=m1+m2=m+m=2m.
- The position vectors are r1 and r2.
- Thus, the center of mass can be calculated as:
RCM=12m(mr1+mr2)
RCM=12mm(r1+r2)=r1+r22
RCM=r1+r22
Topper's Solved these Questions
Similar Questions
Knowledge Check
The centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particlesThe position of centre of mass of a system of particles does not depend upon
Amasses of particlesBforces on particlesCposition of the particlesDrelative distance between the particlesWhich of the following points is the likely position of the centre of mass of the system shown in Fig.
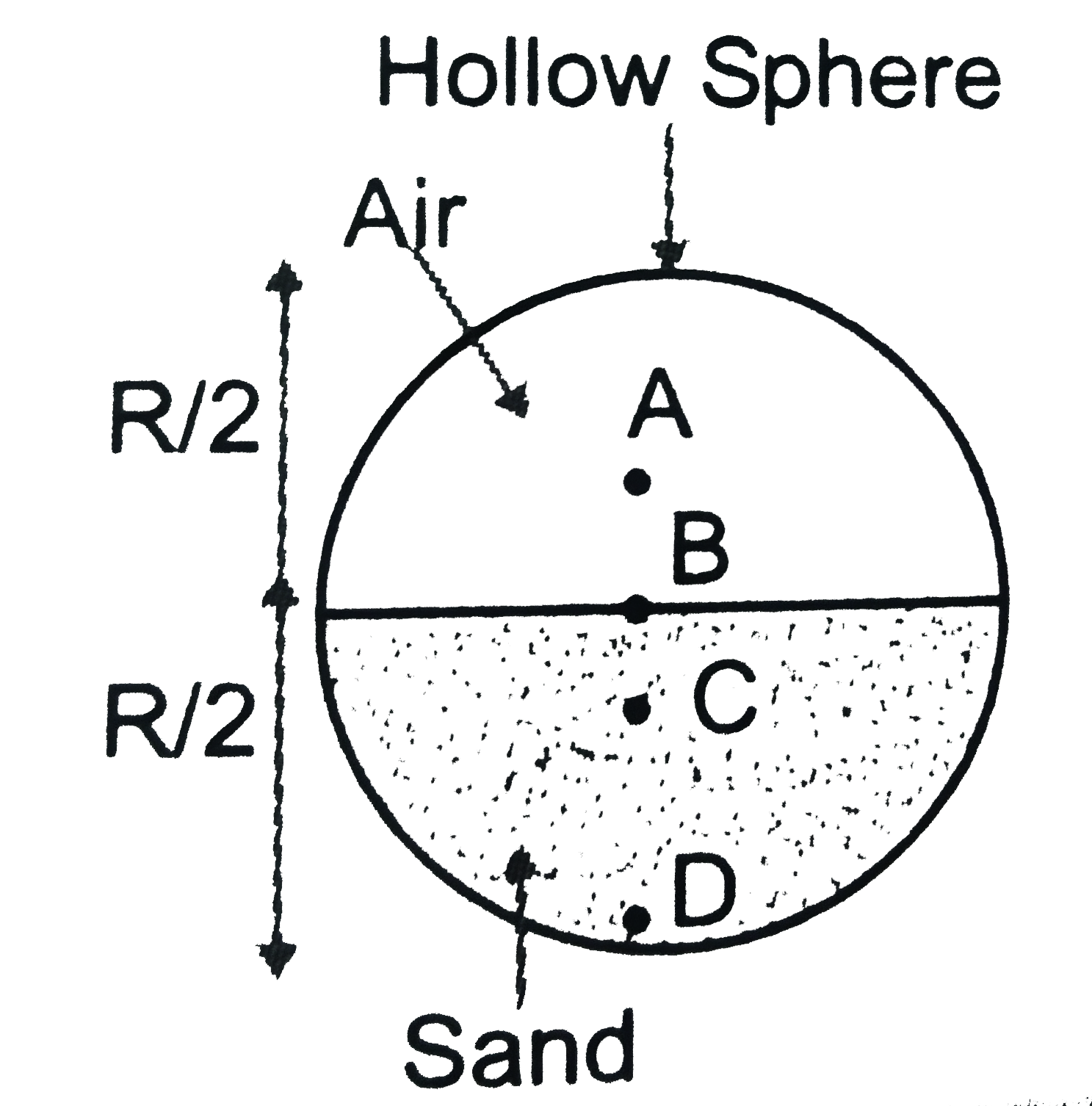 AABBCCDD
AABBCCDD
The position vector of a particle with respect to origin "0" is →r.If the torque acting on the particle is zero,then
View SolutionStatement-1 : The centre of mass of a system of n particles is the weighted average of the position vector of the n particles making up the system
. Statement-2 : The position of the centre of mass of a system is independent of coordinate system
View SolutionObtain an expression for the position vector of centre of mass of a system of n particles.
View SolutionObtain an expression for the position vector of centre of mass of a two particle system.
View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in figure?

View Solution
