If d represents the bond length, then select the correct relation.
dN2=dN+2anddO2=dO+2
dN2<dN+2anddO2>dO+2
dN2<dN+2anddO2<dO+2
dN2>dN+2anddO2=dO+2
The correct Answer is:B
To determine the correct relation of bond lengths for the molecules N2, N2+, O2, and O2+, we will analyze the bond order for each species using molecular orbital theory.
1. Determine the number of electrons in each molecule:
- N2: Contains 14 electrons (7 from each nitrogen atom).
- N2+: Contains 13 electrons (one electron is removed from N2).
- O2: Contains 16 electrons (8 from each oxygen atom).
- O2+: Contains 15 electrons (one electron is removed from O2).
2. Fill the molecular orbitals for N2:
- The molecular orbital configuration for N2 is:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^2 \pi_{2p_x}^*^0 \pi_{2p_y}^*^0
- Bonding electrons: 10 (from σ and π orbitals)
- Antibonding electrons: 4 (from σ* and π* orbitals)
- Bond Order (N2):
Bond Order=(10−4)2=3
3. Fill the molecular orbitals for N2+:
- The molecular orbital configuration for N2+ is similar to N2 but with one less electron:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^1 \pi_{2p_x}^*^0 \pi_{2p_y}^*^0
- Bonding electrons: 9
- Antibonding electrons: 4
- Bond Order (N2+):
Bond Order=(9−4)2=2.5
4. Fill the molecular orbitals for O2:
- The molecular orbital configuration for O2 is:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^2 \pi_{2p_x}^*^1 \pi_{2p_y}^*^1
- Bonding electrons: 10
- Antibonding electrons: 6
- Bond Order (O2):
Bond Order=(10−6)2=2
5. Fill the molecular orbitals for O2+:
- The molecular orbital configuration for O2+ is:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^2 \pi_{2p_x}^*^1 \pi_{2p_y}^*^0
- Bonding electrons: 10
- Antibonding electrons: 5
- Bond Order (O2+):
Bond Order=(10−5)2=2.5
6. Compare bond orders to determine bond lengths:
- Higher bond order indicates shorter bond length. Thus, we have:
- N2 (Bond Order = 3) > N2+ (Bond Order = 2.5)
- O2 (Bond Order = 2) < O2+ (Bond Order = 2.5)
7. Final Relation of Bond Lengths:
- The order of bond lengths from shortest to longest is:
N2<N2+<O2+<O2
- N2: Contains 14 electrons (7 from each nitrogen atom).
- N2+: Contains 13 electrons (one electron is removed from N2).
- O2: Contains 16 electrons (8 from each oxygen atom).
- O2+: Contains 15 electrons (one electron is removed from O2).
- The molecular orbital configuration for N2 is:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^2 \pi_{2p_x}^*^0 \pi_{2p_y}^*^0
- Bonding electrons: 10 (from σ and π orbitals)
- Antibonding electrons: 4 (from σ* and π* orbitals)
- Bond Order (N2):
Bond Order=(10−4)2=3
- The molecular orbital configuration for N2+ is similar to N2 but with one less electron:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^1 \pi_{2p_x}^*^0 \pi_{2p_y}^*^0
- Bonding electrons: 9
- Antibonding electrons: 4
- Bond Order (N2+):
Bond Order=(9−4)2=2.5
- The molecular orbital configuration for O2 is:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^2 \pi_{2p_x}^*^1 \pi_{2p_y}^*^1
- Bonding electrons: 10
- Antibonding electrons: 6
- Bond Order (O2):
Bond Order=(10−6)2=2
- The molecular orbital configuration for O2+ is:
\sigma_{1s}^2 \sigma_{1s}^*^2 \sigma_{2s}^2 \sigma_{2s}^*^2 \sigma_{2p_z}^2 \pi_{2p_x}^2 \pi_{2p_y}^2 \pi_{2p_x}^*^1 \pi_{2p_y}^*^0
- Bonding electrons: 10
- Antibonding electrons: 5
- Bond Order (O2+):
Bond Order=(10−5)2=2.5
- Higher bond order indicates shorter bond length. Thus, we have:
- N2 (Bond Order = 3) > N2+ (Bond Order = 2.5)
- O2 (Bond Order = 2) < O2+ (Bond Order = 2.5)
- The order of bond lengths from shortest to longest is:
N2<N2+<O2+<O2
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One or More
Select the correct relations :
A−ΔS=(∂E∂T)P×nFB(∂E∂T)P=ΔG−ΔHTCΔS=(∂E∂tT)P×nFD(∂E∂T)P=(∂ΔS∂T)P - Question 2 - Select One
Select correct relation.
A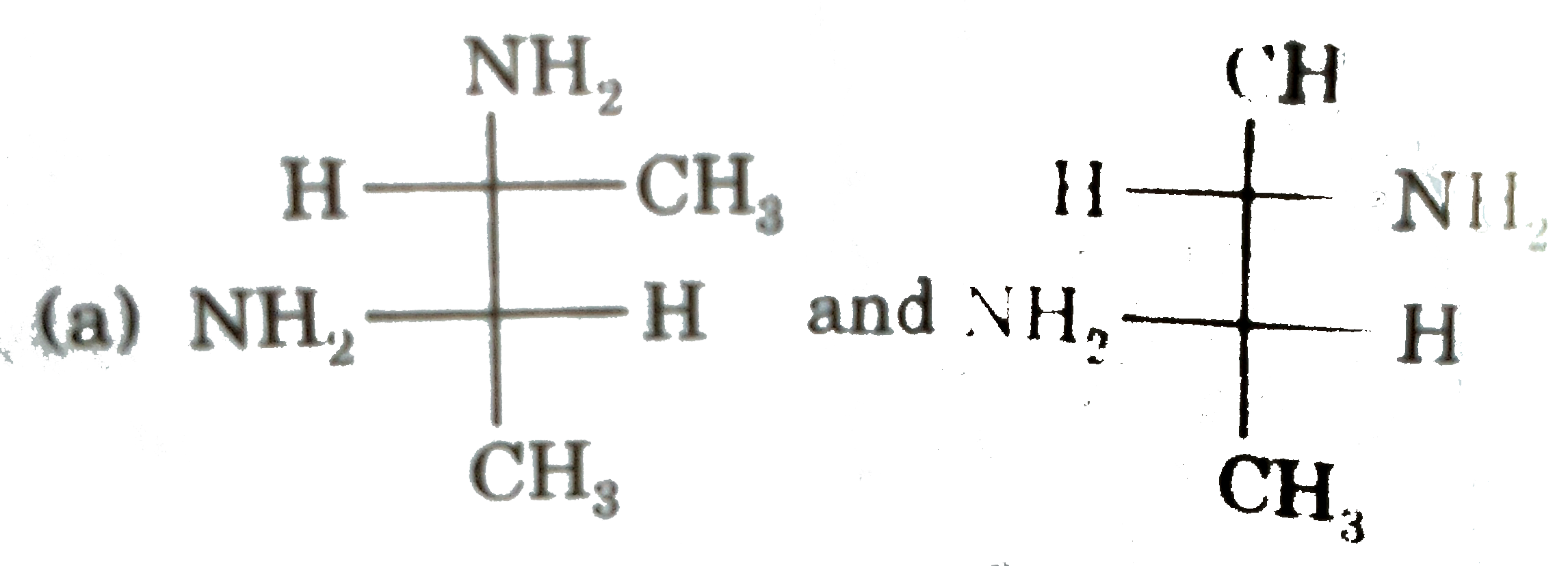
B
C
D
- Question 3 - Select One
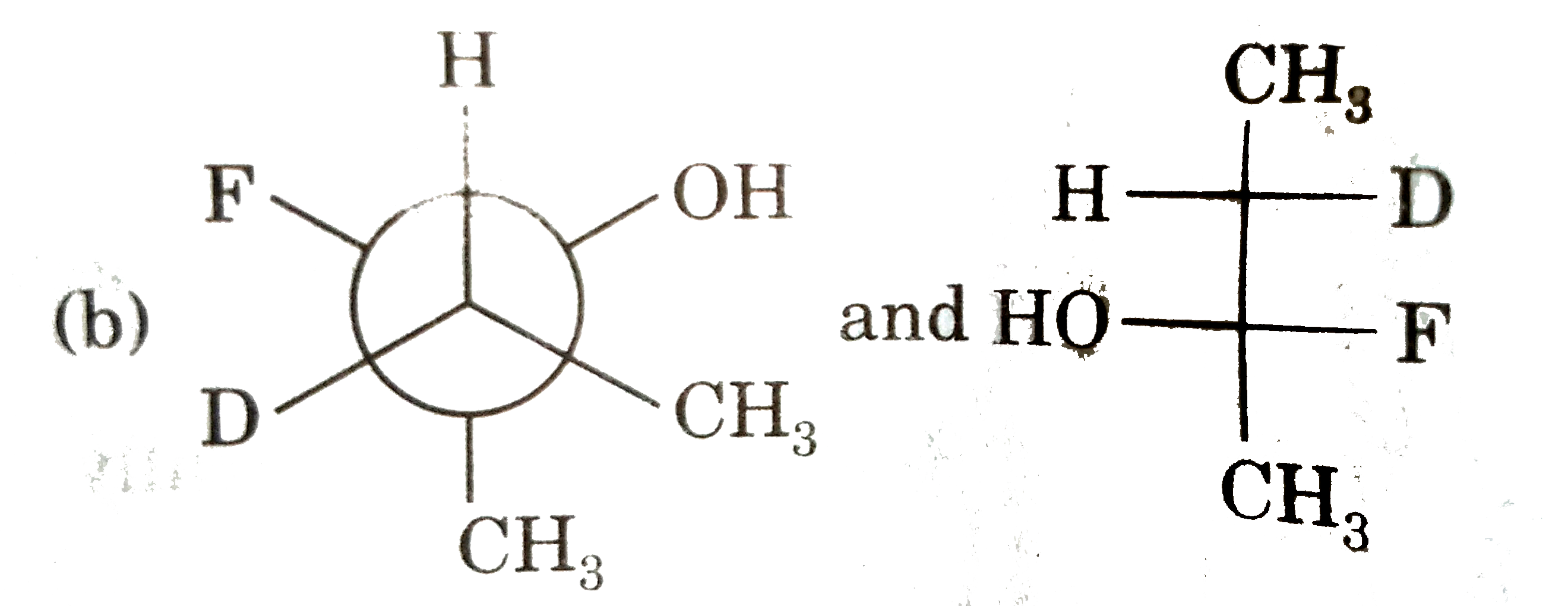Compare the bond lengths and select the correct option:
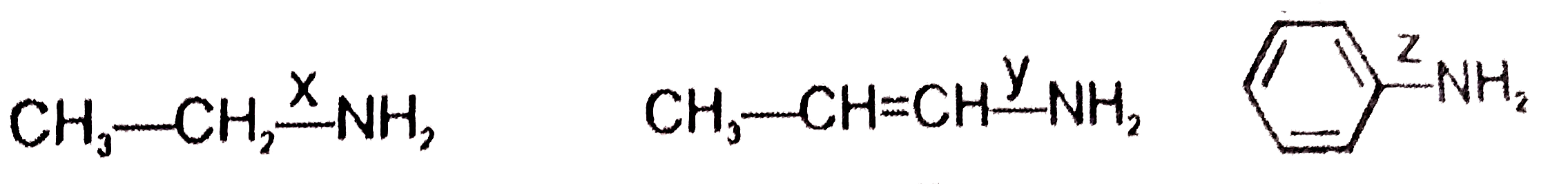Ax=y=zBx>y>zCx<y<zDx>y=z
Correct order of bond length is
View SolutionCorrect order of bond length is
View SolutionIf in an allene system, nodal plane of first π−bond and last π-bond are in same plane then select the correct statement.
View Solution
For the above transitions in a H−like species, select the correct relation(s) :View SolutionThe given figure represents the histology of of a striated muscle. Identify the parts labelled as A, B, C and D, and select the correct option.
View Solution