If ABC is a triangle such that A=(1,2) and B=(5,5) with BC=9 and AC =12 units , then slope of altitude CD is (D is a point on BC)
−43
43
34
−34
The correct Answer is:A
Step by step video, text & image solution for If ABC is a triangle such that A=(1,2) and B=(5,5) with BC=9 and AC =12 units , then slope of altitude CD is (D is a point on BC) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Exercise 16videos
CIRCLE
- BOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Exercise 26videos
CIRCLE
- BOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Numerical Based2videos
CIRCLE
- BOOK - FIITJEECHAPTER - AREAEXERCISE - Numerical Based3videos
AREA
- BOOK - FIITJEECHAPTER - COMPLEX NUMBEREXERCISE - NUMERICAL BASED3videos
COMPLEX NUMBER
Similar Questions
Knowledge Check
- Question 1 - Select One
The mid-points of sides AB and AC of a triangle ABC are respectively X and Y. If (BC+XY)=12units, then the value of (BC−XY) is :
A2 unitsB6 unitsC8 unitsD4 units - Question 2 - Select One
D is a point on the side BC of △ABC such that ∠ADC=∠BAC. If CA = 12 cm and BC = 16 cm, then the length of CD is :
A12 cmB6 cmC8 cmD9 cm - Question 3 - Select One
The mid-points of sides AB and AC of a triangle ABC are respectively X and Y. If (BC+XY)=12 units, then the value of (BC−XY) is
A2 unitsB6 unitsC8 unitsD4 units
△ABC is an isoscles triangle with AB= AC= 13 cm and the length of altitude from A on BC is 5 cm, find BC.
View SolutionThe extremities of the base of an isosceles triangle ΔABC are the points A(2.0) and B(0,1). If the equation of the side AC is x=2 then the slope of the side BC
View SolutionIf ΔABC is an isosceles triangle such that AB=AC, then altitude AD from A on BC bisects BC (Fig.43).
View SolutionΔABC is right-angled at A and AD⊥BC. If BC=13cmandAC=5cm, find the ratio of areas of ΔABCandΔADC.
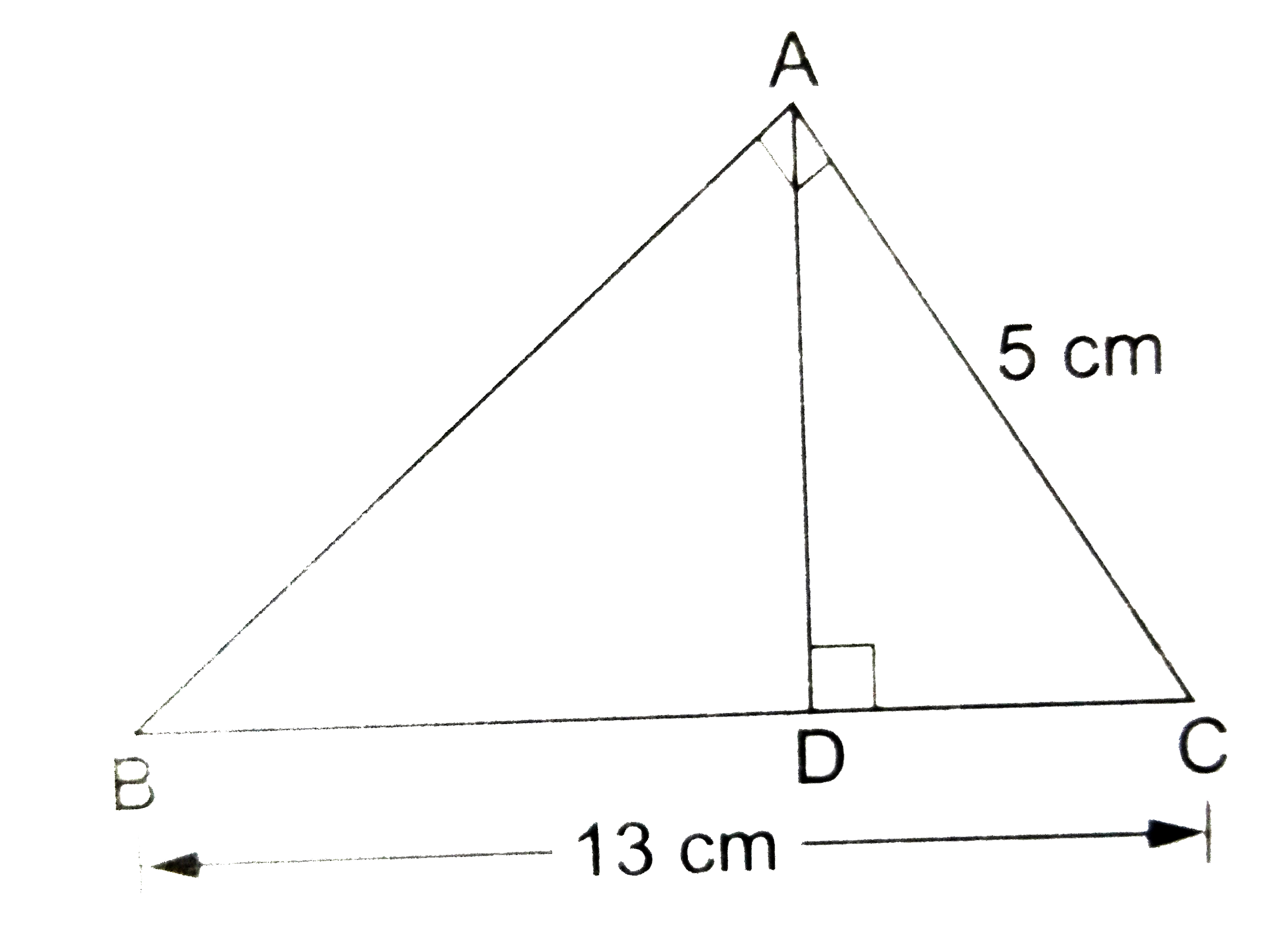 View Solution
View SolutionIn a triangle ABC, BC = 5 cm, AC = 12 cm and AB = 13 cm. The length of the altitude drawn from B on AC is -----
View Solution

