From a point P (α,β) a pair of tangents PQ and PR are drawn to circle x2+y2−2x−2y−2=0 such that QR is chord of contact. Considering PQ and PR are adjacent sides a parallelogram PQRS is formed . Equation of chord of contact QR is x =0, S1 and S2 be the circles circumscribing the triangle PQR and QRS.
Co-ordinate of point P(α,β) is equal to
(3,2)
(2,3)
(-3,1)
none of these
The correct Answer is:C
Topper's Solved these Questions
- CIRCLEBOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Numerical Based
2 Videos
- CIRCLEBOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Assignment Problems (Objective) Level -II
15 Videos
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Numerical Based
3 Videos
- COMPLEX NUMBERBOOK - FIITJEECHAPTER - COMPLEX NUMBEREXERCISE - NUMERICAL BASED
3 Videos
Similar Questions
Knowledge Check
From a point P (α,β) a pair of tangents PQ and PR are drawn to circle x2+y2−2x−2y−2=0 such that QR is chord of contact. Considering PQ and PR are adjacent sides a parallelogram PQRS is formed . Equation of chord of contact QR is x =0, S1 and S2 be the circles circumscribing the triangle PQR and QRS.
Equation of circle S1=0 isAx2+y2+4x−2y−2=0Bx2+y2−2x+2y−2=0Cx2+y2+2x−2y−2=0Dnone of theseFrom a point P perpendicular tangents PQ and PR are drawn to ellipse x2+4y2=4, then locus of circumcentre of triangle PQR is
Ax2+y2=165(x2+4y2)2Bx2+y2=516(x2+4y2)2Cx2+4y2=165(x2+y2)2Dx2+4y2=165(x2+y2)2Let the tangents PQ and PR are drawn to y2=4ax from any point P on the line x+4a=0. The angle subtended by the chord of contact QR at the vertex of the parabola y2=4ax is
Aπ4Bπ3Cπ2Dπ6
From the point P(−1,−2),PQ and PR are the tangents drawn to the circle x2+y2−6x−8y=0 .Then angle subtended by QR at the centre of the circle is
View SolutionLet P be a variable point. From P tangents PQ and PR are drawn to the circle x2+y2=b2 if QR always touch the parabola y2=4ax then locus ofP is
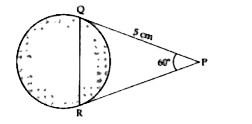
View SolutionIn the give figure ,PQ and PR are tangents to the given circle such that PQ =5 cm and ∠QPR=60∘. The length of chord QR is
View SolutionLet the tangents PQ and PR are drawn to y2=4ax from any point P on the line x+4a=0. The angle subtended by the chord of contact QR at the vertex of the parabola y2=4ax is
View SolutionLet PQR be a right - angled isosceles triangle , right angled at P(2,1). If the equation of the line QR is 2x+y=3, then the equation representing the pair of lines PQ and PR is
View Solution
