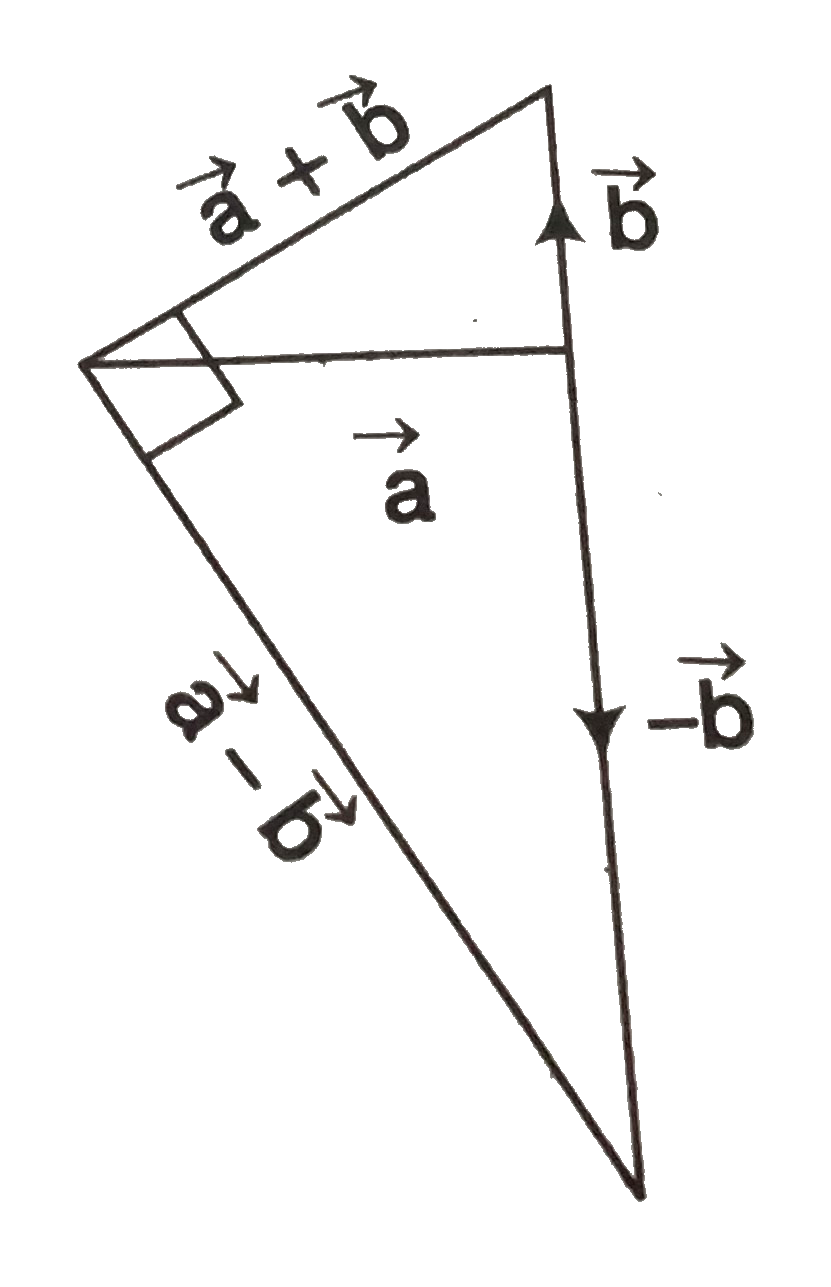
The formula ${(\to a + \to b)}^{2} = \to a^{2} + \to b^{2} + 2 \to a \times \to b$ is valid for non-zero vectors $\to a and \to b$ .

Video Solution

Text Solution

Verified by Experts

${(\to a + \to b)}^{2} = (\to a + \to b) . (\to a + \to b)$
$= \to a^{2} + \to b^{2} + 2 \to a . \to b$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

BOOK - NCERT EXEMPLARCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Three Dimensional Geometry
46videos
THREE DIMENSIONAL GEOMETRY

Similar Questions

Knowledge Check

Question 1 - Select One
If $\to a and \to b$ are non-zero, non-collinear vectors such that $| \to a | = 2, \to a \cdot \to b = 1$ and angle between $\to a and \to b$ is $\frac{π}{3}$ . If $\to r$ is any vector such that $\to r \cdot \to a = 2, \to r \cdot \to b = 8, (\to r + 2 \to a - 10 \to b) \cdot (\to a \times \to b) = 4 \sqrt{3}$ and satisfy to $\to r + 2 \to a - 10 \to b = λ (\to a \times \to b)$ , then $λ$ is equal to :
A $\frac{1}{2}$
B2
C $\frac{1}{4}$
DNone of these

NCERT EXEMPLAR-VECTOR ALGEBRA-Vector Algebra

Home
Ask Doubt
Profile