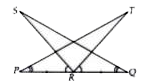
In Fig. 8.40, prove that Δs OAM and OBN are congruent and hence prove that AM=BN.
Step by step video & image solution for In Fig. 8.40, prove that Delta s OAM and OBN are congruent and hence prove that AM= BN. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Prove that ΔSQRandΔTPR are congruent and SR = TR.
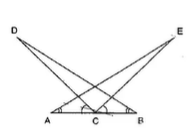
View SolutionIn Figure, AC=BC, ∠DCA=∠ECB and ∠DBC=EAC. Prove that triangle DBC and EAC are congruent, and hence DC=EC and BD=AE
View SolutionIn the given fig. KN, PA and PB are tangents to the circle. Prove that : KN=AK+BN.

View SolutionBC is an equilateral triangle. A circle is drawn with centre A so that it cuts AB and AC at points M and N respectively. Prove that BN = CM
View SolutionIn triangle ABC, the sides AB and AC are equal. If P is a point on AB and Q is a point on AC such that AP = AQ, prove that :
(i) triangle APC and AQB are congruent.
(ii) triangle BPC and CQB are congruent.

View SolutionProve that, angles inscribed in the same are arc congruent.

View Solution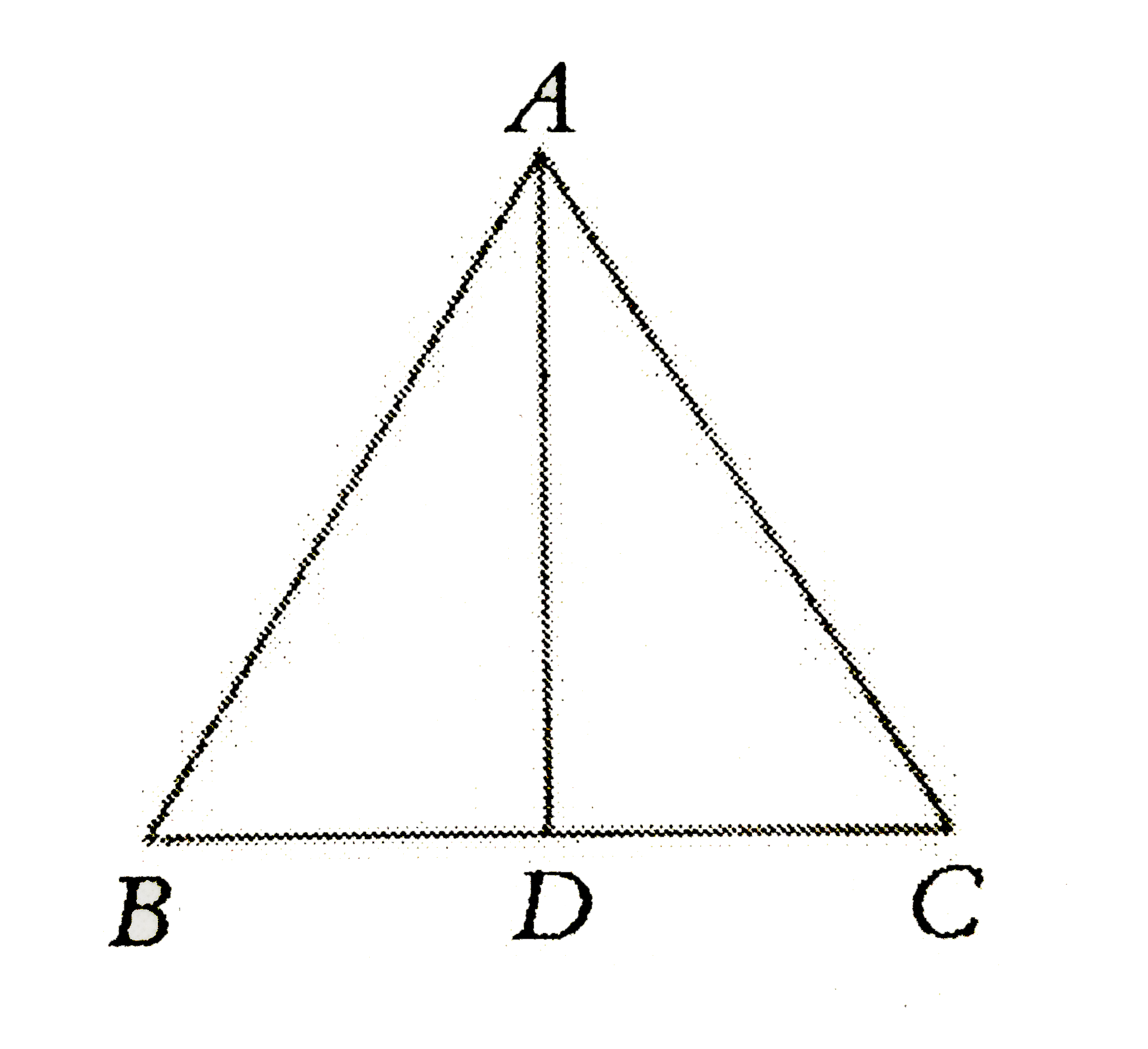
In the given figure, AD is the bisector of ∠BAC. Prove that triangles ABD and ADC are congruent, if AB=AC.
View SolutionIf in a ΔABC, prove that Δ<s24
View SolutionIn Fig. 4.123, ABCD is a trapezium with AB∣∣DC. If ΔAED is similar to ΔBEC, prove that AD=BC.
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that ∠PSQand∠PTR are right angles
If OS and RT intersect at M, prove that the triangles PTM and PSM are congruent.
View Solution
