Find the coordinates of the point R on the line segment joining the points P(−1,3) and Q (2,5) such that PR =35 PQ.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

According to the question ,
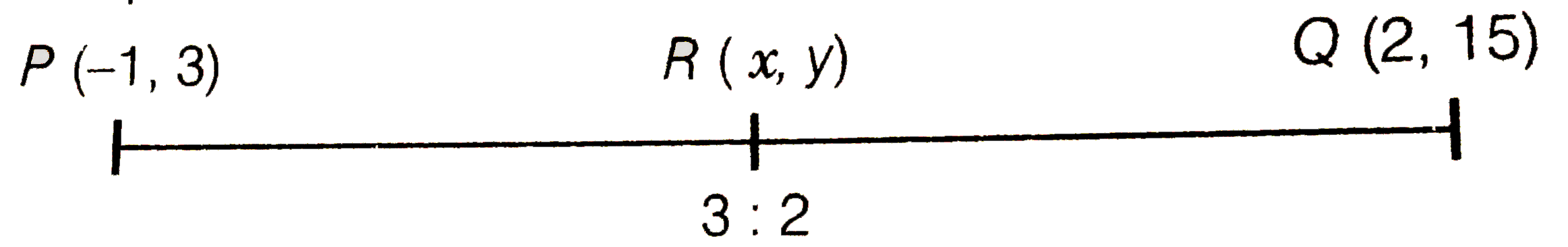
ocr_image
Given that , PR =35PQ
⇒PQPR=53
⇒PR+RQPR=53
⇒1+RQPR=53
⇒PQPR=53−1=23
∴PQ:PR=2:3
or ∴PR:RQ=3:2
Suppose , R (x,y) be the point which divides the line segment joining the points P (-1,3) and Q(2,5) in the ration 3:2.
∴(x,y)={3(2)+2(−1)3+2,3(5)+2(3)3+2}
[∵ by internal section formula , ∴(x,y)={m2x1+m1x2m1+m2,m2y1+m1y2m1+m2}]
=(6−25,15+65)=(45,215)
Hence , the required coordinates of the point R is (45,215).

Updated on:21/07/2023
|
Class 10MATHSCOORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The mid point of the line segment joining the points (−5,7)and(−1,3) is

    A(−3,7)
    B(−3,5)
    C(−1,5)
    D(5,−3)

  • The coordinates of the point P dividing the line segment joining the points A(1, 3) and B(4, 6) in the ratio 2:1 is

    A(2, 4)
    B(3, 5)
    C(4, 2)
    D(5, 3)