Two parallel lines are everywhere the same distance apart.
The correct Answer is:T
To determine whether the statement "Two parallel lines are everywhere the same distance apart" is true or false, we can analyze the properties of parallel lines.
1. Understanding Parallel Lines:
- Begin by defining what parallel lines are. Parallel lines are lines in a plane that do not meet; they are always the same distance apart.
2. Drawing Parallel Lines:
- Draw two straight lines on a piece of paper. Label them as Line L1 and Line L2. Ensure that they are parallel to each other.
3. Extending the Lines:
- Extend both lines in both directions. This means you should draw arrows at both ends of each line to indicate that they continue infinitely.
4. Measuring the Distance:
- Choose a point on Line L1 and draw a perpendicular line to Line L2. This perpendicular line represents the shortest distance between the two lines.
- Measure this distance.
5. Checking Consistency:
- Now, pick another point on Line L1 and repeat the process by drawing another perpendicular line to Line L2. Measure this distance as well.
- You will find that this distance is the same as the previous measurement.
6. Conclusion:
- Since the distance between the two parallel lines remains constant regardless of where you measure it, we can conclude that the statement "Two parallel lines are everywhere the same distance apart" is true.
Final Statement:
Thus, the statement is True.
---
- Begin by defining what parallel lines are. Parallel lines are lines in a plane that do not meet; they are always the same distance apart.
- Draw two straight lines on a piece of paper. Label them as Line L1 and Line L2. Ensure that they are parallel to each other.
- Extend both lines in both directions. This means you should draw arrows at both ends of each line to indicate that they continue infinitely.
- Choose a point on Line L1 and draw a perpendicular line to Line L2. This perpendicular line represents the shortest distance between the two lines.
- Measure this distance.
- Now, pick another point on Line L1 and repeat the process by drawing another perpendicular line to Line L2. Measure this distance as well.
- You will find that this distance is the same as the previous measurement.
- Since the distance between the two parallel lines remains constant regardless of where you measure it, we can conclude that the statement "Two parallel lines are everywhere the same distance apart" is true.
Thus, the statement is True.
Topper's Solved these Questions
- CONSTRUCTIONS ( USING RULER AND A PAIR OF COMPASSES )Book:RS AGGARWALChapter:CONSTRUCTIONS ( USING RULER AND A PAIR OF COMPASSES )Exercise:TEST PAPER-14 (C.) Fill in the blanks.
Explore 5 Videos
- CONCEPT OF PERIMETER AND AREA Book:RS AGGARWALChapter:CONCEPT OF PERIMETER AND AREA Exercise:Test Paper 21 (Fill in the Blanks)
Explore 6 Videos
- DATA HANDLING Book:RS AGGARWALChapter:DATA HANDLING Exercise:EXERCISE 22
Explore 10 Videos
Similar Questions
Which of the following statements are true and which are false ?
Two parallel lines are everwhere the same distance apart.
View SolutionTwo equal smooth sphere of radius a are moving with equal speed u in opposite directions along parallel lines which are a distance a apart. The coeficient of restitution between them is 1/3.Find their velocities after impact.
View Solution
Knowledge Check
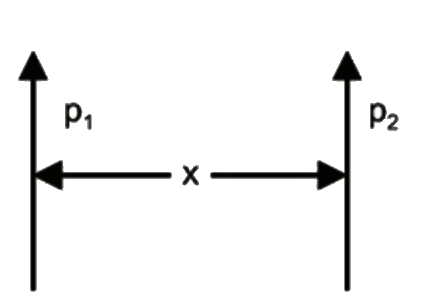
Two long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper , as shown. The variation of the magnetic field B along the line XX is given by
A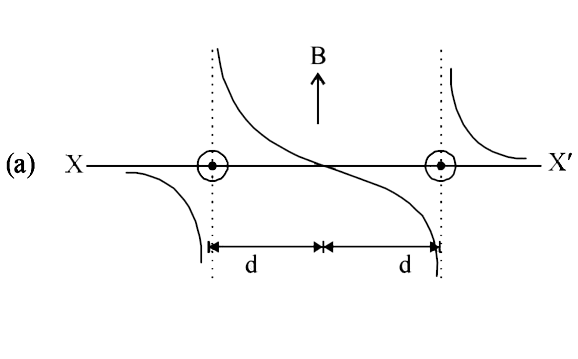 B
B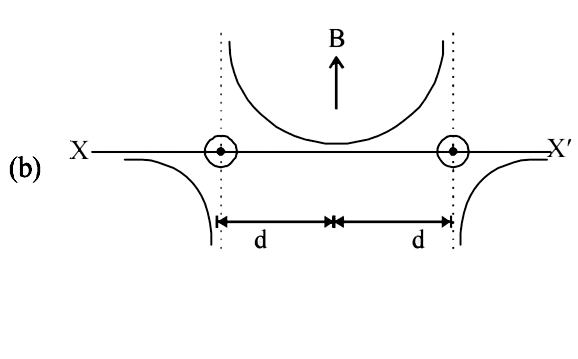 C
C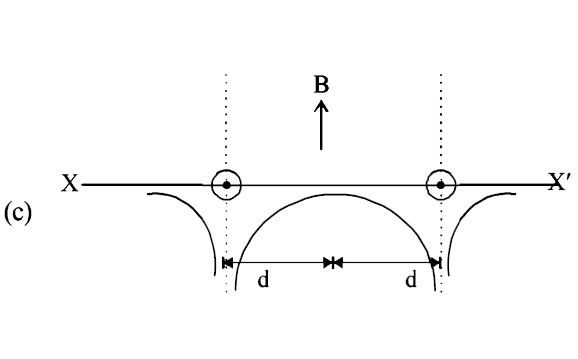 D
D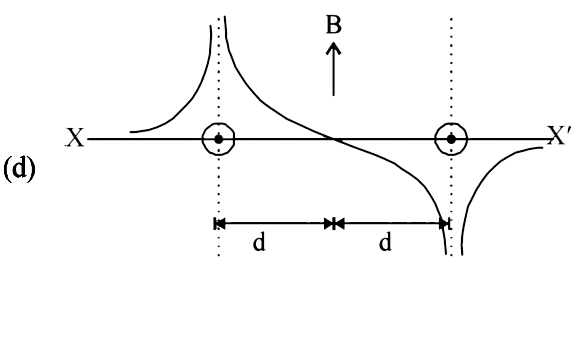
Two long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper , as shown. The variation of the magnetic field B along the line XX is given by
A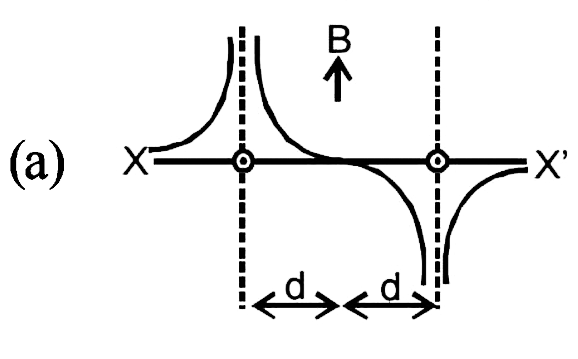 B
B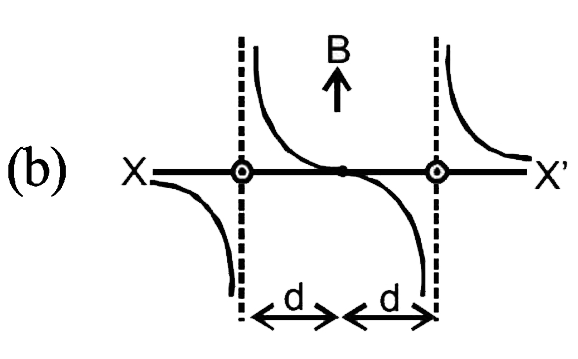 C
C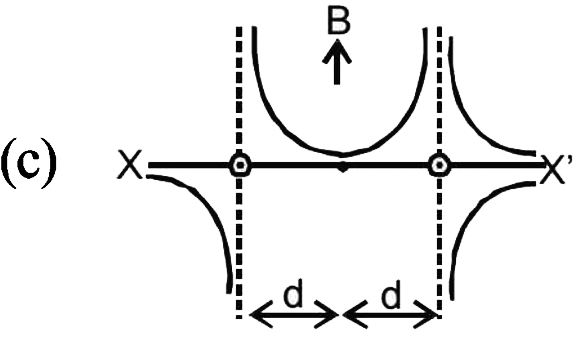 D
D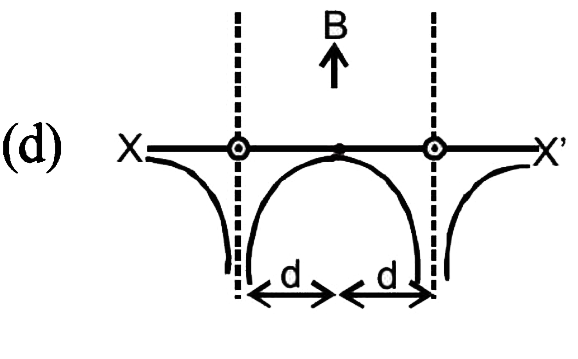
In a trapezium, the two non-parallel sides are equal in length, each being of 5 units. The parallel sides are at a distance of 3 units apart. If the smaller side of the parallel sides is of length 2 units, then the sum of the diagonals of the trapezium is
A10√5 unitsB6√5 unitsC5√5 unitsD3√5 units
Draw two parallel lines at a distance of 2.2 cm apart.
View SolutionPand Q are two like parallel forces. If two equal and opposite forces S, in any two parallel lines at a distance: b apart in the plane of Pand Q, are combined with them, then their resultant is displaced by a distance bSP+Q.
View SolutionA line l intersects a pair of parallel lines. The exterior angles on the same side of line l are in the ratio of 5:4. The measure of the bigger angle of the two is……………………..
View SolutionWhich of the following statements are true (T) and which are false (F)? Give reasons. (i)If two lines are intersected by a transversal, then corresponding angles are equal. (ii)If two parallel lines are intersected by a transversal, then alternate interior angles are equal. (iii)Two lines perpendicular to the same line are perpendicular to each other. (iv)Two lines parallel to the same line are parallel to each other. (v)If two parallel lines are intersected by a transversal, then the interior angle on the same side of the transversal are equal.
View SolutionFind the force of interaction of two dipoles , if the two dipole moments are parallel to each other and placed at a distance x apart
View Solution