Two parallel lines l and m are cut by a transversal t. If the interior angles of the same side of t are (2x−8)∘ and(3x−7)∘ , find the measure of each of these angles.
To solve the problem, we need to find the measures of the two interior angles formed by the transversal cutting through the two parallel lines. The angles are given as (2x−8)∘ and (3x−7)∘.
1. Understand the Property of Interior Angles:
When two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary. This means that the sum of these angles equals 180∘.
2. Set Up the Equation:
We can write the equation based on the property of supplementary angles:
(2x−8)+(3x−7)=180
3. Combine Like Terms:
Combine the terms on the left side:
2x+3x−8−7=180
This simplifies to:
5x−15=180
4. Solve for x:
Add 15 to both sides of the equation:
5x=180+15
5x=195
Now, divide both sides by 5:
x=1955=39
5. Find the Measure of Each Angle:
Substitute x=39 back into the expressions for the angles:
- For the first angle:
2x−8=2(39)−8=78−8=70∘
- For the second angle:
3x−7=3(39)−7=117−7=110∘
6. Conclusion:
The measures of the angles are:
- First angle: 70∘
- Second angle: 110∘
Final Answer:
- The measure of the first angle is 70∘.
- The measure of the second angle is 110∘.
When two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary. This means that the sum of these angles equals 180∘.
We can write the equation based on the property of supplementary angles:
(2x−8)+(3x−7)=180
Combine the terms on the left side:
2x+3x−8−7=180
This simplifies to:
5x−15=180
Add 15 to both sides of the equation:
5x=180+15
5x=195
Now, divide both sides by 5:
x=1955=39
Substitute x=39 back into the expressions for the angles:
- For the first angle:
2x−8=2(39)−8=78−8=70∘
- For the second angle:
3x−7=3(39)−7=117−7=110∘
The measures of the angles are:
- First angle: 70∘
- Second angle: 110∘
- The measure of the first angle is 70∘.
- The measure of the second angle is 110∘.
Topper's Solved these Questions
- PROPERTIES OF PARALLEL LINE BOOK - RS AGGARWALCHAPTER - PROPERTIES OF PARALLEL LINE EXERCISE - EXERCISE 14
15 Videos
- PROFIT AND LOSSBOOK - RS AGGARWALCHAPTER - PROFIT AND LOSSEXERCISE - Test paper
9 Videos
- PROPERTIES OF TRIANGLESBOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-D
18 Videos
Similar Questions
Knowledge Check
If two parallel lines are cut by a transversal, then the alternate interior angles are equal
ATRUEBFALSECCannot be determinedDNone of theseIf two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementaryThe ratio of two interior angles on the same side of the transversal is 2:3 , the measure of difference of both the angles is -
A36∘B180∘C72∘D108∘
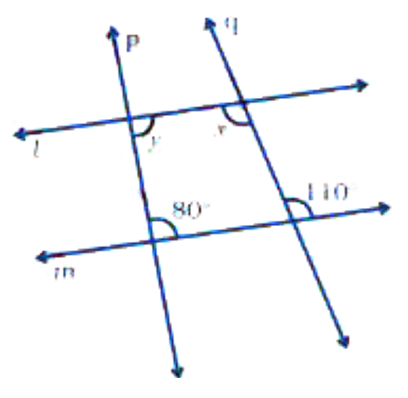
In Fig.5.66 , two parallel lines l and m are cut by two transversals p and q . Determine the values of x and y .
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionFill in the blanks in each of the following to make the statement true: (i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are.... (ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are... (iii) Two lines perpendicular to the same line are.... to each other. (iv) Two lines parallel to the same line are .......... to each other. (v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the line are... (vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180,then the line are .......
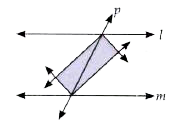
View SolutionTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
View Solution