In a△DEF, if ∠E=105∘ and ∠F=40∘,find ∠D
To find angle D in triangle DEF, where angle E is 105° and angle F is 40°, we can follow these steps:
1. Understand the Sum of Angles in a Triangle:
The sum of all angles in a triangle is always 180°. This means that in triangle DEF:
angle D+angle E+angle F=180°
2. Substitute the Known Angles:
We know that angle E = 105° and angle F = 40°. We can substitute these values into the equation:
angle D+105°+40°=180°
3. Combine the Known Angles:
Now, we can add the angles E and F together:
105°+40°=145°
So, the equation now looks like:
angle D+145°=180°
4. Isolate angle D:
To find angle D, we need to isolate it on one side of the equation. We can do this by subtracting 145° from both sides:
angle D=180°−145°
5. Calculate angle D:
Now we perform the subtraction:
angle D=35°
Final Answer:
Thus, angle D in triangle DEF is 35°.
---
The sum of all angles in a triangle is always 180°. This means that in triangle DEF:
angle D+angle E+angle F=180°
We know that angle E = 105° and angle F = 40°. We can substitute these values into the equation:
angle D+105°+40°=180°
Now, we can add the angles E and F together:
105°+40°=145°
So, the equation now looks like:
angle D+145°=180°
To find angle D, we need to isolate it on one side of the equation. We can do this by subtracting 145° from both sides:
angle D=180°−145°
Now we perform the subtraction:
angle D=35°
Thus, angle D in triangle DEF is 35°.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-B
8 Videos
- PROPERTIES OF TRIANGLESBOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-C
7 Videos
- PROPERTIES OF TRIANGLESBOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-D
18 Videos
- PROPERTIES OF PARALLEL LINE BOOK - RS AGGARWALCHAPTER - PROPERTIES OF PARALLEL LINE EXERCISE - EXERCISE 14
15 Videos
- RATION AND PROPORTION BOOK - RS AGGARWALCHAPTER - RATION AND PROPORTION EXERCISE - Test papers
18 Videos
Similar Questions
Knowledge Check
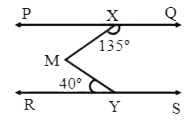
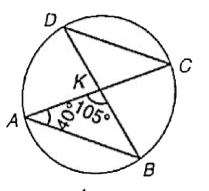
In the figure above (not to scale), ABCDE is symmetrical about AF. If ∠C=90∘ and ∠BAF=45∘, then find the ∠E.A90∘B105∘C135∘D130∘In the given figure, ∠CAB=40∘and∠AKB=105∘. Find ∠KCD :
 A65∘B35∘C40∘D72∘
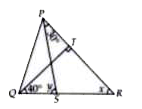
A65∘B35∘C40∘D72∘In figure, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find value of y-x
 A80∘B50∘C30∘D130∘
A80∘B50∘C30∘D130∘
If △ABCand△DEF are similar triangles such that ∠A=45∘and∠F=56∘, then find angle C
View SolutionABCD is a kite in which AB=AD and CB=CD. If ∠ABD=30∘and∠BDC=40∘, then find ∠A+∠C.
View SolutionIn Fig. 5.49, AB||CD, AF||ED, ∠AFC=68∘ and ∠FED=42∘. Find ∠EFD.
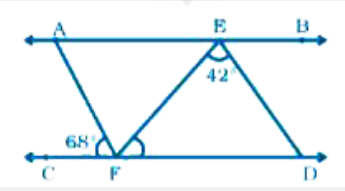
View SolutionIn the adjoining figure, if ∠ACB=40∘, ∠DPB=120∘, then find ∠CBD.

View Solution
In the figure above ∠QPS=2∠SPR,∠Q=∠R+40∘and∠PSR=120∘. Find ∠QPR
View Solution