In △ABC, AB=AC and AD⊥BC,BE⊥AC and CF⊥AB. Then △ABC is symmetrical about
AD
BE
CF
None of these
The correct Answer is:A
To solve the problem, we need to determine the line of symmetry in triangle ABC, given that AB = AC and certain perpendiculars are drawn from points A, B, and C to the opposite sides.
1. Identify the Triangle:
We start by drawing triangle ABC where AB = AC. This means triangle ABC is an isosceles triangle.
Hint: Remember that in an isosceles triangle, two sides are equal.
2. Draw the Perpendiculars:
We are given that:
- AD is perpendicular to BC
- BE is perpendicular to AC
- CF is perpendicular to AB
We will draw these perpendiculars accordingly.
Hint: Perpendiculars form right angles (90 degrees) with the sides they intersect.
3. Analyze the Symmetry:
In an isosceles triangle, the line of symmetry is the perpendicular drawn from the vertex angle (A in this case) to the base (BC). This line divides the triangle into two equal halves.
Hint: The line of symmetry in an isosceles triangle always passes through the vertex opposite the base.
4. Conclusion:
Since AD is the perpendicular from A to BC, it acts as the line of symmetry for triangle ABC. Therefore, triangle ABC is symmetrical about line AD.
Hint: When identifying the line of symmetry, look for the line that divides the triangle into two congruent parts.
Final Answer:
Triangle ABC is symmetrical about line AD.
We start by drawing triangle ABC where AB = AC. This means triangle ABC is an isosceles triangle.
We are given that:
- AD is perpendicular to BC
- BE is perpendicular to AC
- CF is perpendicular to AB
In an isosceles triangle, the line of symmetry is the perpendicular drawn from the vertex angle (A in this case) to the base (BC). This line divides the triangle into two equal halves.
Since AD is the perpendicular from A to BC, it acts as the line of symmetry for triangle ABC. Therefore, triangle ABC is symmetrical about line AD.
Triangle ABC is symmetrical about line AD.
Topper's Solved these Questions
- REFLECTION AND ROTATIONAL SYMMETRYBOOK - RS AGGARWALCHAPTER - REFLECTION AND ROTATIONAL SYMMETRYEXERCISE - Exercise A(True / False)
7 Videos
- REFLECTION AND ROTATIONAL SYMMETRYBOOK - RS AGGARWALCHAPTER - REFLECTION AND ROTATIONAL SYMMETRYEXERCISE - Exercise B
12 Videos
- REFLECTION AND ROTATIONAL SYMMETRYBOOK - RS AGGARWALCHAPTER - REFLECTION AND ROTATIONAL SYMMETRYEXERCISE - Exercise B
12 Videos
- RATIONAL NUMBERSBOOK - RS AGGARWALCHAPTER - RATIONAL NUMBERSEXERCISE - TEST PAPER -(4)
17 Videos
- SIMPLE INTEREST BOOK - RS AGGARWALCHAPTER - SIMPLE INTEREST EXERCISE - test perper 12 D
1 Videos
Similar Questions
Knowledge Check
In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤ADΔABC,AB=AC and BA is produced to D such that AC = AD. Then the ∠BCD is
A100∘B60∘C80∘D90∘ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
A100∘B60∘C80∘D90∘
In △ ABC, AD is a median. Prove that AB + AC > 2AD
View SolutionIn △ABC, ∠ABC=90∘ and BD⊥AC. if AD=4 cm and CD=5 cm, then BD is equal to:
△ABC में, ∠ABC=90∘ और BD⊥AC है| यदि AD=4 cm और CD=5 cm तो BD किसके समान होगा?
View SolutionIn the given fig; AB⊥BC,FG⊥BC, and DE⊥AC. Prove that △ADE~△GCF.
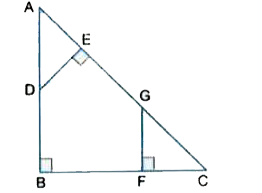
View SolutionIn the given figure, DB⊥BC,DE⊥ABandAC⊥BC.
Prove that BEDE=ACBC

View SolutionIn △ABC, AD⊥BC and BE⊥AC, AD and BE intersect each other at F. If BF = AC, then the measure of ∠ABC is:
त्रिभुज ABC में, AD⊥BC है तथा BE⊥AC है | AD और BD एक दूसरे को F पर काटते है | यदि BF = AC है, तो ∠ABC का माप क्या होगा ?
View Solution
