A Cuboid has ____ rectangular faces, ____edges and _____vertices.
The correct Answer is:6,12,8
To solve the question regarding the properties of a cuboid, we will identify the number of rectangular faces, edges, and vertices step by step.
1. Identify the Rectangular Faces:
- A cuboid is a three-dimensional shape that has six faces. All of these faces are rectangles.
- To visualize this, think of a box. The top and bottom faces are rectangles, and the four side faces are also rectangles.
- Therefore, the total number of rectangular faces in a cuboid is 6.
2. Count the Edges:
- An edge is a line segment where two faces meet.
- A cuboid has edges along the length, width, and height.
- For each pair of opposite faces, there are 4 edges. Since there are 3 pairs of opposite faces (top-bottom, front-back, left-right), we can calculate the total number of edges:
- 4 edges (top-bottom) + 4 edges (front-back) + 4 edges (left-right) = 12 edges.
3. Determine the Vertices:
- A vertex is a point where three edges meet.
- In a cuboid, there are 8 corners (or vertices).
- Each corner of the cuboid represents a vertex where three edges intersect.
- Therefore, the total number of vertices in a cuboid is 8.
Final Answer:
- A cuboid has 6 rectangular faces, 12 edges, and 8 vertices.
- A cuboid is a three-dimensional shape that has six faces. All of these faces are rectangles.
- To visualize this, think of a box. The top and bottom faces are rectangles, and the four side faces are also rectangles.
- Therefore, the total number of rectangular faces in a cuboid is 6.
- An edge is a line segment where two faces meet.
- A cuboid has edges along the length, width, and height.
- For each pair of opposite faces, there are 4 edges. Since there are 3 pairs of opposite faces (top-bottom, front-back, left-right), we can calculate the total number of edges:
- 4 edges (top-bottom) + 4 edges (front-back) + 4 edges (left-right) = 12 edges.
- A vertex is a point where three edges meet.
- In a cuboid, there are 8 corners (or vertices).
- Each corner of the cuboid represents a vertex where three edges intersect.
- Therefore, the total number of vertices in a cuboid is 8.
- A cuboid has 6 rectangular faces, 12 edges, and 8 vertices.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - THREE -DIMENSIONAL SHAPESEXERCISE - Exercise( True / False)5videos
THREE -DIMENSIONAL SHAPES
- BOOK - RS AGGARWALCHAPTER - THREE -DIMENSIONAL SHAPESEXERCISE - Execise1videos
THREE -DIMENSIONAL SHAPES
- BOOK - RS AGGARWALCHAPTER - THREE -DIMENSIONAL SHAPESEXERCISE - Execise1videos
THREE -DIMENSIONAL SHAPES
- BOOK - RS AGGARWALCHAPTER - SIMPLE INTEREST EXERCISE - test perper 12 D1videos
SIMPLE INTEREST
- BOOK - RS AGGARWALCHAPTER - UNITARY METHODEXERCISE - TEST PAPER -918videos
UNITARY METHOD
Similar Questions
Knowledge Check
- Question 1 - Select One
Can a polyhedron have 10 faces, 20 edges and 15 vertices? Check using Euler's formula.
AYesBNoCCannot be determinedDNone of the above
A square pyramid has_____________faces,____________edges and ___________vertices.
View SolutionIf f, e, and v represent the number of rectangular faces, number of edges and number of vertices repectively of a cuboid, then the values of f, e, and v respectively are _________.
View SolutionA polyhedron can have 10 faces, 20 edges and 15 vertices.
View SolutionWrite (T) for True and (F) for false:
(ii) A Cube has 6 faces , 12 edges and 8 vertices.View SolutionThe figure 12.3 has _________vertices, _____________edges and _____________faces.
 View Solution
View SolutionA triangular prism has 5 faces, 9 edges and 6 vertices. state true or false
View SolutionComplete the table below by writing the number of faces, edges and vertices each figure has :
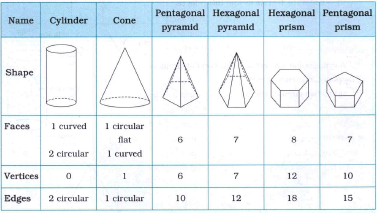 View Solution
View Solution

