A rectangular field is 50 m by 40 m. It has two roads through its centre, running parallel toits sides. The width of the longer and the shorter roads are 2 m and 2.5-m-respectivelyFind the area of the roads and the area of the remaining portion of the field.
The correct Answer is:195m2.1805m2
To solve the problem step by step, we will calculate the area of the roads and the area of the remaining portion of the rectangular field.
Step 1: Calculate the area of the rectangular field.
The area of a rectangle is given by the formula:
Area=Length×Breadth
For the given rectangular field:
- Length = 50 m
- Breadth = 40 m
Calculating the area:
Area of the field=50m×40m=2000m2
Step 2: Calculate the area of the longer road.
The longer road runs parallel to the length of the rectangle and has a width of 2 m.
Using the area formula:
- Length of the road = 50 m (same as the length of the field)
- Width of the road = 2 m
Calculating the area:
Area of the longer road=50m×2m=100m2
Step 3: Calculate the area of the shorter road.
The shorter road runs parallel to the breadth of the rectangle and has a width of 2.5 m.
Using the area formula:
- Length of the road = 40 m (same as the breadth of the field)
- Width of the road = 2.5 m
Calculating the area:
Area of the shorter road=40m×2.5m=100m2
Step 4: Calculate the total area of the roads.
The total area of the roads is the sum of the areas of both roads:
Total area of the roads=Area of longer road+Area of shorter road=100m2+100m2=200m2
Step 5: Subtract the overlapping area.
The area where the two roads overlap (the intersection) is a rectangle formed by the widths of both roads:
- Length of the overlap = 2 m (width of the longer road)
- Width of the overlap = 2.5 m (width of the shorter road)
Calculating the area of the overlap:
Area of overlap=2m×2.5m=5m2
Now, we subtract the overlapping area from the total area of the roads:
Total area of the roads after removing overlap=200m2−5m2=195m2
Step 6: Calculate the area of the remaining portion of the field.
To find the area of the remaining portion of the field, we subtract the area of the roads from the area of the entire field:
Area of remaining portion=Area of field−Total area of roads
Area of remaining portion=2000m2−195m2=1805m2
Final Answers:
- Area of the roads: 195 m²
- Area of the remaining portion of the field: 1805 m²
The area of a rectangle is given by the formula:
Area=Length×Breadth
For the given rectangular field:
- Length = 50 m
- Breadth = 40 m
Area of the field=50m×40m=2000m2
The longer road runs parallel to the length of the rectangle and has a width of 2 m.
- Length of the road = 50 m (same as the length of the field)
- Width of the road = 2 m
Area of the longer road=50m×2m=100m2
The shorter road runs parallel to the breadth of the rectangle and has a width of 2.5 m.
- Length of the road = 40 m (same as the breadth of the field)
- Width of the road = 2.5 m
Area of the shorter road=40m×2.5m=100m2
The total area of the roads is the sum of the areas of both roads:
Total area of the roads=Area of longer road+Area of shorter road=100m2+100m2=200m2
The area where the two roads overlap (the intersection) is a rectangle formed by the widths of both roads:
- Length of the overlap = 2 m (width of the longer road)
- Width of the overlap = 2.5 m (width of the shorter road)
Area of overlap=2m×2.5m=5m2
Total area of the roads after removing overlap=200m2−5m2=195m2
To find the area of the remaining portion of the field, we subtract the area of the roads from the area of the entire field:
Area of remaining portion=Area of field−Total area of roads
Area of remaining portion=2000m2−195m2=1805m2
- Area of the roads: 195 m²
- Area of the remaining portion of the field: 1805 m²
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20C16videos
MENSURATION
- BOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20D24videos
MENSURATION
- BOOK - RS AGGARWALCHAPTER - MENSURATIONEXERCISE - EXERCISE 20A20videos
MENSURATION
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 1311videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - PERCENTAGE EXERCISE - TEST PAPER16videos
PERCENTAGE
Similar Questions
A rectangular field is 50 m by 40 m. It has two roads through its centre, running parallel to its sides. The widths of the longer and shorter roads are 1.8 m and 2.5 m respectively. Find the area of the roads and the area of the remaining portion of the field.
View SolutionLength and breadth of a rectangular field are 50m and 15m respectively. Find the ratio of the length to the breadth of the field.
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular field is 90m×50m. Inside the field there is path of width 5 m bordering the field. What is the area of the path ?
A1450sqmB1100sqmC1000sqmD1300sqm - Question 2 - Select One
A rectangular grass plot 80m×60m has two roads, each 10 m wide, running in the middle of it, one parallel to length and the other parallel to breadth.Find the area of the roads.
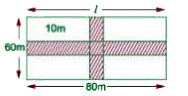 ARs. 380BRs. 385CRs. 400Dnone of these
ARs. 380BRs. 385CRs. 400Dnone of these
If the radius and height of a road roller are 0.5 m and 1.4 m respectively, then find the area of field pressed in 100 rotations.
View SolutionA rectangular lawn is 30 m by 20 m. It has two roads each 2 m wide running in the middle of it one parallel to the length and the other parallel to the breadth. Find the area of the roads.
View SolutionA rectangular lawn 70 m by 50 m has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of constructing the roads at Rs.120 per m2.
View Solutionthe longer side of a rectangular hall is 24 m and the length of its diagonal is 26 m. Find the area of the hall .
View SolutionA rectangular lawn is 60 m by 40 m and has two roads. each 5 m wide running in the middle of it, one parallel to its length and the other parallel to the breadth, as shown in the figure. Find the cost of constructing the roads at Rs. 80 per m2.
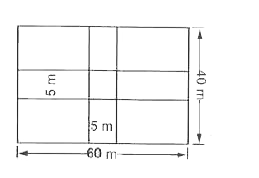 View Solution
View SolutionA rectangular lawn 55m by 35m has two roads each 4m wide running in the middle of itone parallel to the length and the other parallel to the breadth. What is the cost of gravelling the roads at 75 paise per square metre?
View Solution

