(a) What is Brownian motion ? Draw a diagram to show the movement of a particle (like a pollen grain) during Brownian motion.
(b) In a beam of sunlight entering a room, we can sometimes see dust particles moving in a haphazard way in the air. Why do these dust particles move ?
Step by step video & image solution for (a) What is Brownian motion ? Draw a diagram to show the movement of a particle (like a pollen grain) during Brownian motion. (b) In a beam of sunlight entering a room, we can sometimes see dust particles moving in a haphazard way in the air. Why do these dust particles move ? by Chemistry experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATTER IN OUR SURROUNDINGS BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - MATTER IN OUR SURROUNDINGS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
6 Videos
- MATTER IN OUR SURROUNDINGS BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - MATTER IN OUR SURROUNDINGS EXERCISE - SHORT ANSWER TYPE QUESTIONS
13 Videos
- IS MATTER AROUND US PURE BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - IS MATTER AROUND US PURE EXERCISE - NCERT BOOK PAGE 24
1 Video
- MODEL TEST PAPER 1BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - MODEL TEST PAPER 1EXERCISE - SECTION B
3 Videos
Similar Questions
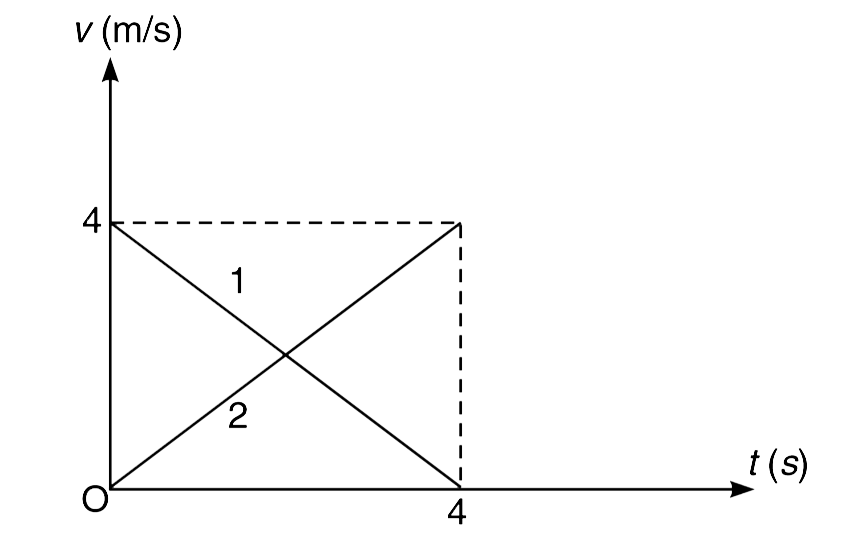
The velocity time graph for two particles (1 and 2) moving along X axis is shown in fig. At time t=0, both were at origin.
(a) During first 4 second of motion what is maximum separation between the particles? At what time the separation is maximum?
(b) Draw position (x) vs time (t) graph for the particles for the given interval.
View Solution(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.

(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.
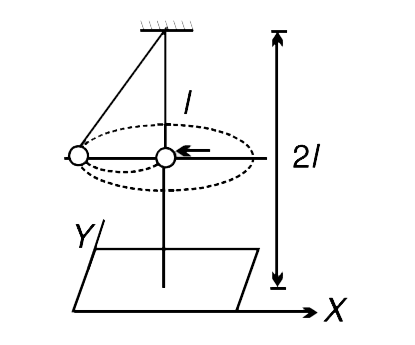
(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ?
View Solution
Knowledge Check
The French physicist Louis de Broglie in 1924 postulated that matter , like radiation , should exhibit dual behaviour. He proposed the following relationship between the wavelenght lambda of a material particle , its linear momentum p and planck cosntant h.
λ=hp=hmv
The de Broglie relation implies that the wavelength of a partices should decreases as its velocity increases. It also implies that the for a given velocity heavir particule should have shorter wavelenght than lighter particles. The waves associated with particles in motin are called matter waves or de Broglie waves.
These waves differ from the electromagnetic waves as they
(i) have lower velocities
have no electrical and magnetic fields and
are not emitted by the particle under consideration.
The experimental confirmation of the de Broglie relation was obtained when Davisson and Germer. in
1927, observed that a beam of electrons is diffracted by a nickel arystal. As diffarceted by a nickel . As diffraction is a characteristic
property of waves, hence the beam of electron dehaves as a wave, as proposed by de Broglie.
Werner Heisenberg cobnsiderd the imits of how precisely we can measure propoerties of an electron or
other microscopic particle like electron. he determined that there is accurately we measure the momentum of a
particle, the less accurately we can determine its position . The converse is laso true . The is summed up
in what we now call the "Hesienberg uncertainty princple: It isimpossibble to determine simultameously ltbr> and percisely both the momentum ans position of particle . The product of uncertainly in the position,
Deltax and the ncertainly in the momentum Delta(mv) mudt be greater than or equal to h4π i.e.
ηΔxΔ(mv)≥h4π
The correct order of wavelenght of Hydrogen (.1H1) Deuterium (.1H2) and Tritium (.1H3) moving withsame kinetic energy is.AλH>λD>λTBλH=λD=λTCλH<λD<λTDλH<λD>λTWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=α⋅x4(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
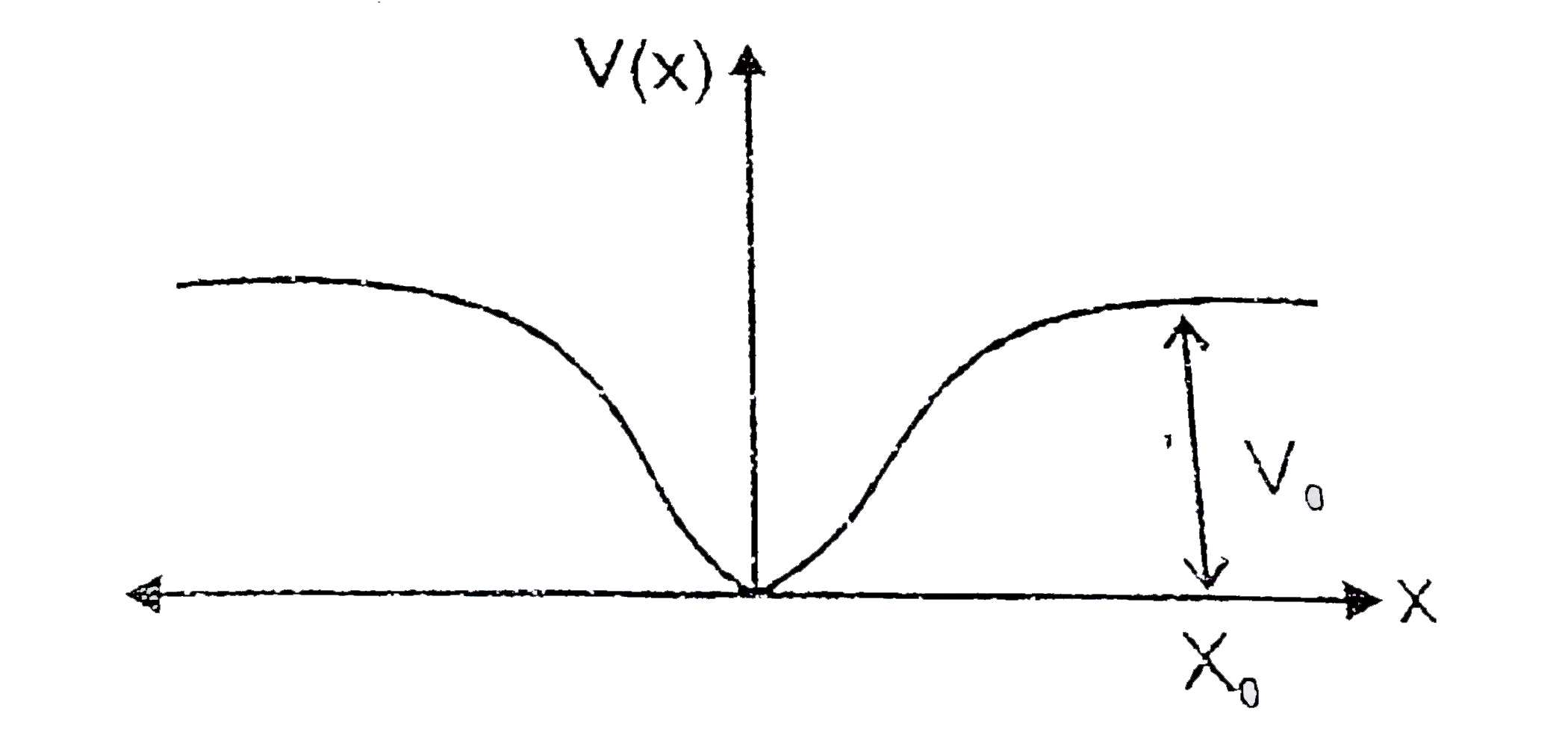
If the total energy of the particle is E, it will perform is periodic motion why if :AE<0BE>0CV0>E>0DE>V0In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is E=−3B216A, and it is known that the motion is radial only then the velocity is zero atAr03B2r03Cr0D2r05
In one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision

View SolutionA cyclotron is device for accelerating ions and charged particles. It was developed by Lawerence in 1932.
The heart of the appritus consists of a split metal pillbox. Figure sHOws top and front views of the halves called dees. A rapidly oscilating potential difference is applied between the Dees. This produces an oscilating electric field in the gap between the dees, the region inside each dee being essentially free of electric field. The Dees are enclosed in an evaccutaed container, and the entire unit is placed in a uniform magnetic field B whose direction is normal to the plane Of Dees, A charged particle of mass 'm' and charge 'q' in the gap between the dees, it moves with constant speed in a semi-circle.
The period of uniform circular motion is T=2πmqB and is independant of speed. If the time-period of the oscilating elctric field is equal to this time, then the charged particle will be accelerated again and again

Answer the following questions (consider the mass of particles remains constant during motion):
The maximum radius of the dees required if deutron is to acquire 100 MeV of energy in the above question is:
View SolutionIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QThe graph shows the psition of a hard ball with respect to time .The hard ball hits and rebounds on the hard surface .Ehich of the following graph represent the correct variation with repect to time?

View SolutionIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision

View SolutionA cyclotron is device for accelerating ions and charged particles. It was developed by Lawerence in 1932.
The heart of the appritus consists of a split metal pillbox. Figure sHOws top and front views of the halves called dees. A rapidly oscilating potential difference is applied between the Dees. This produces an oscilating electric field in the gap between the dees, the region inside each dee being essentially free of electric field. The Dees are enclosed in an evaccutaed container, and the entire unit is placed in a uniform magnetic field B whose direction is normal to the plane Of Dees, A charged particle of mass 'm' and charge 'q' in the gap between the dees, it moves with constant speed in a semi-circle.
The period of uniform circular motion is T=2πmqB and is independant of speed. If the time-period of the oscilating elctric field is equal to this time, then the charged particle will be accelerated again and again

Answer the following questions (consider the mass of particles remains constant during motion):
A cyclotron has been adjusted to accelereted deutrons. It is now to be adjusted to accelerate other particles , for this following changes may be made:
(a) In order to keep the frequency of oscillating electric field same, the magnetic field is halved for proton
(b) If the magnetic field remain unchanged, the oscillation frequency of electric field should be halved for α particle
(c ) If the magnetic field remain unchanged, the oscillation frequency of electric field should be double for proton
(d) If the frequency of oscillating electric field is kept same, the magnetic field should be kept same for α particle
View Solution