Find angle θ, 0 < θ < π2 , which increase twice as fast as sine
Video Solution
Text Solution
Let θ increases twice as fast at its sine.
⇒θ=2sinθ
Now, on differentiating both sides w.r.t., we get
d(θ)dt=2.cosθ.d(θ)dt⇒1=2cosθ
⇒12=cosθ⇒cosθ=cosπ3.
So, the required angle is π3
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A shot is fired at an angle θ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection θ.
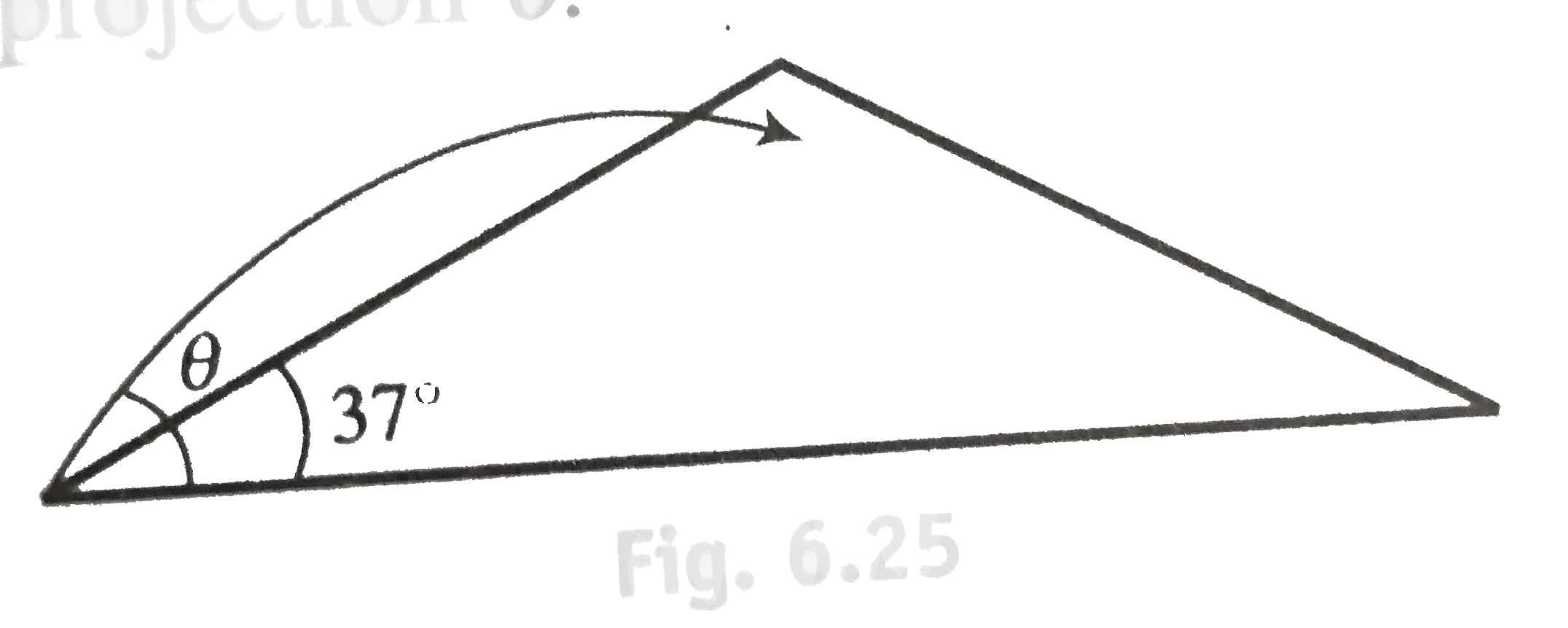Atanθ=25Btanθ=38Ctanθ=32DNone of these
A body is thrown at an angle θ0 with the horizontal such that it attains a speed equal to (√23 times the speed of projection when the body is at half of its maximum height. Find the angle θ0.
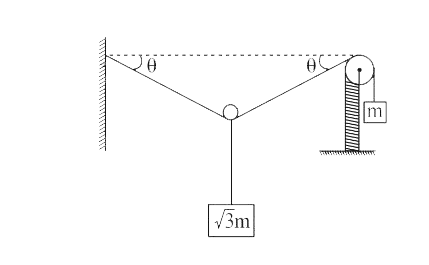
View SolutionThe system is in equilibrium. Find the angle θ
View SolutionAngle of a line with the positive direction of the x-axis is θ . The line is rotated about some point on it in anticlockwise direction by angle 450 and its slope becomes 3. Find the angle θ.
View SolutionFind the angle θ whose cosine is equal to its tangent.
View SolutionTo find the trigonometrical ratios of an angle (−θ) in terms of θ, for all values of θ.
View Solution_S01_021_Q01.png)
Find out pressure at points A and B also find angle θView SolutionA projectile's launch speed is 6.00 times that of its speed at its maximum height. Find the launch angle θ0.
View Solution