A circle touches the parabola y2=4x at (1,2) and also touches its directrix. The y-coordinates of the point of contact of the circle and the directrix is-
√2
2
2√2
4
The correct Answer is:C
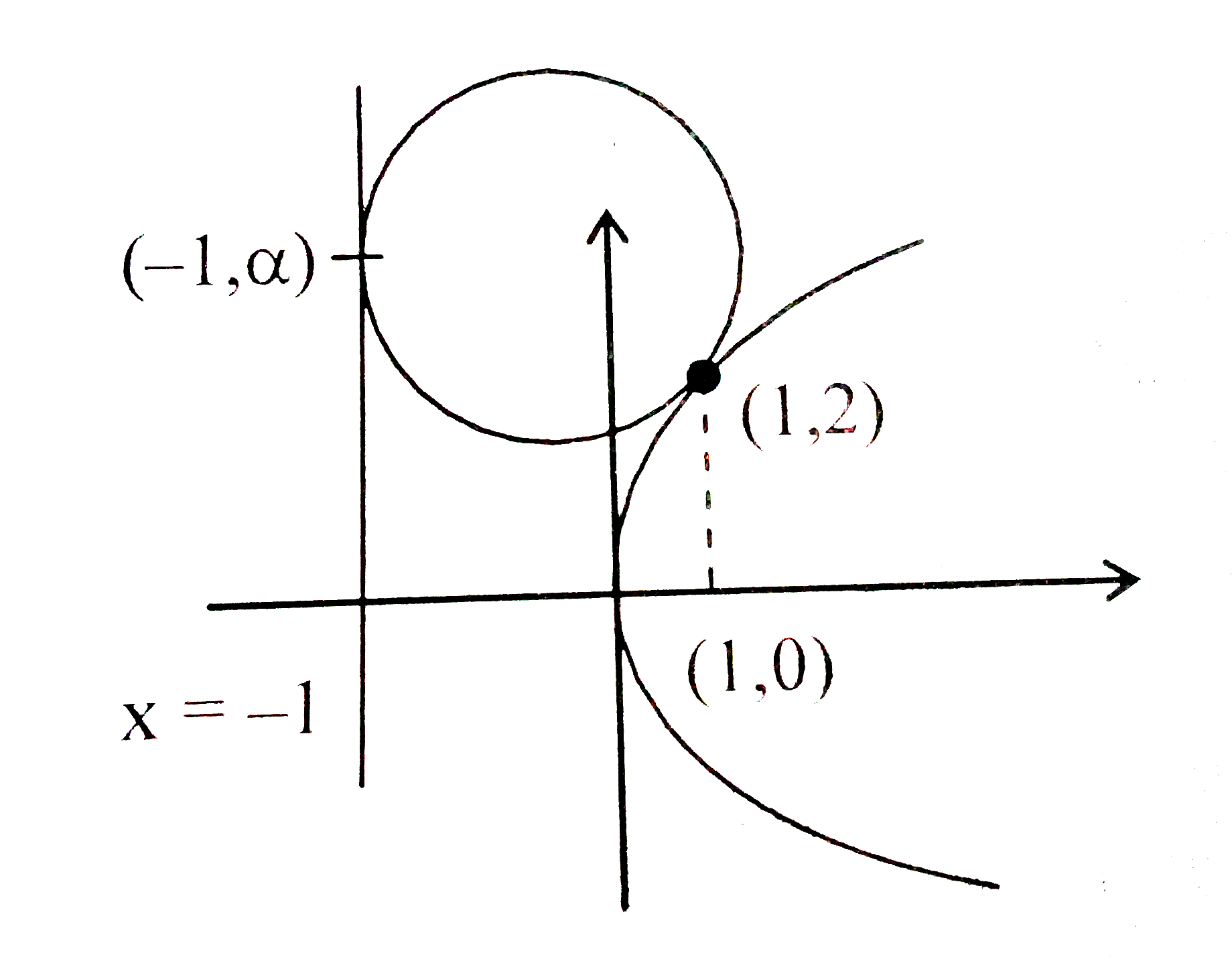
y2=4x
2ydydx=4
mT=2y=22=1
Circle →S+λL=0
(x+1)2+(y−α)2+λ(x+1)=0…..(1)
differentiate
2(x+1)2+2(y−α)dydx+λ=0
x=1,y=2
4+2(2−α)mT+λ=0
λ=2α−8......(2)
(1,2) satisfies eq. (1)
22+(2−α)2+2λ=0
α2−4α+8+2(2α−8)=0
α2=8
α=2√2
Topper's Solved these Questions
Similar Questions
Let f(x) be a quadratic polynomial with f(2)=−2. Then the coefficient of x in f(x) is-
05:34View SolutionLet a, b, c be positive integers such that a√2+bb√2+c is a rational number, then which of the following is always an integer?
04:30View SolutionLet a, b, c be non-zero real roots of the equation x3+ax2+bx+c=0. Then
05:34View SolutionConsider a circle with its centre lying on the focus of the parabola,y^(2)=2px such that it touches the directrix of the parabola.Then a a point of intersection of the circle & the parabola is:
03:05View SolutionA circle touches the parabola y^(2)=4x at (1,2) and also touches its directrix.The y- coordinates of the point of contact of the circle and the directrix is-
03:01View Solution2. A circle, with its centre at the focus of the parabola y? - 4ax and touching its directrix, intersects the parabola at the point (A) (a, 2a) (B) (a,-2a) (D) a/2a 2a
07:44View SolutionThe radius of circle touching parabola y^(2)=x at (1,1) and having directrix of y^(2)=x as its normal is
03:12View SolutionLet a circle touches to the directrix of a parabola y2=2ax has its centre coinciding with the focus of the parabola. Then the point of intersection of the parabola and circle is
03:51View SolutionShow that the circle described on a focal chord of a parabola as diameter touches its directrix .
01:36View SolutionA circle is drawn to pass through the extremities of the latus rectum of the parabola y2=8x. It is given that this circle also touches the directrix of the parabola. Find the radius of this circle.
04:28View SolutionConsider a circle with its centre lying on the focus of the parabola, y^2=2px such that it touches the directrix of the parabola. Then a point of intersection of the circle & the parabola is:
02:57View SolutionA circle is drawn to pass through the extremities of the latus rectum of the parabola y2=8x. It is given that this circle also touches the directrix of the parabola. Find the radius of this circle.
04:21View SolutionLet a circle touches to the directrix of a parabola y ^(2) = 2ax has its centre coinciding with the focus of the parabola. Then the point of intersection of the parabola and circle is
04:15View SolutionCircles are described on any focal chords of a parabola as diameters touches its directrix
08:33View SolutionA circle is drawn to pass through the extremities of the latus rectum of the parabola y2=8x. It is given that this circle also touches the directrix of the parabola. Find the radius of this circle.
03:46View SolutionConsider a circle with its centre lying on the focus of the parabola, y^2=2px such that it touches the directrix of the parabola. Then a point of intersection of the circle & the parabola is:
03:49View Solution

