Consider the regions $A = {(x, y) ∣ x^{2} + y^{2} \leq 100}$ and $= {(x, y) ∣ sin (x + y) > 0}$ in the plane. Then the area of the region $A \cap B$ is -

A

$10 π$

B

$100$

C

$100 π$

D

$50 π$

Text Solution

Verified by Experts

The correct Answer is:D

$x^{2} + y^{2} \leq 100 \to inside of a circle$
$sin (x + y) > 0$
$x + y \in (x, π) \cup (2 π, 3 π) \dots\dots.$
$x + y = c \to equation of a line$

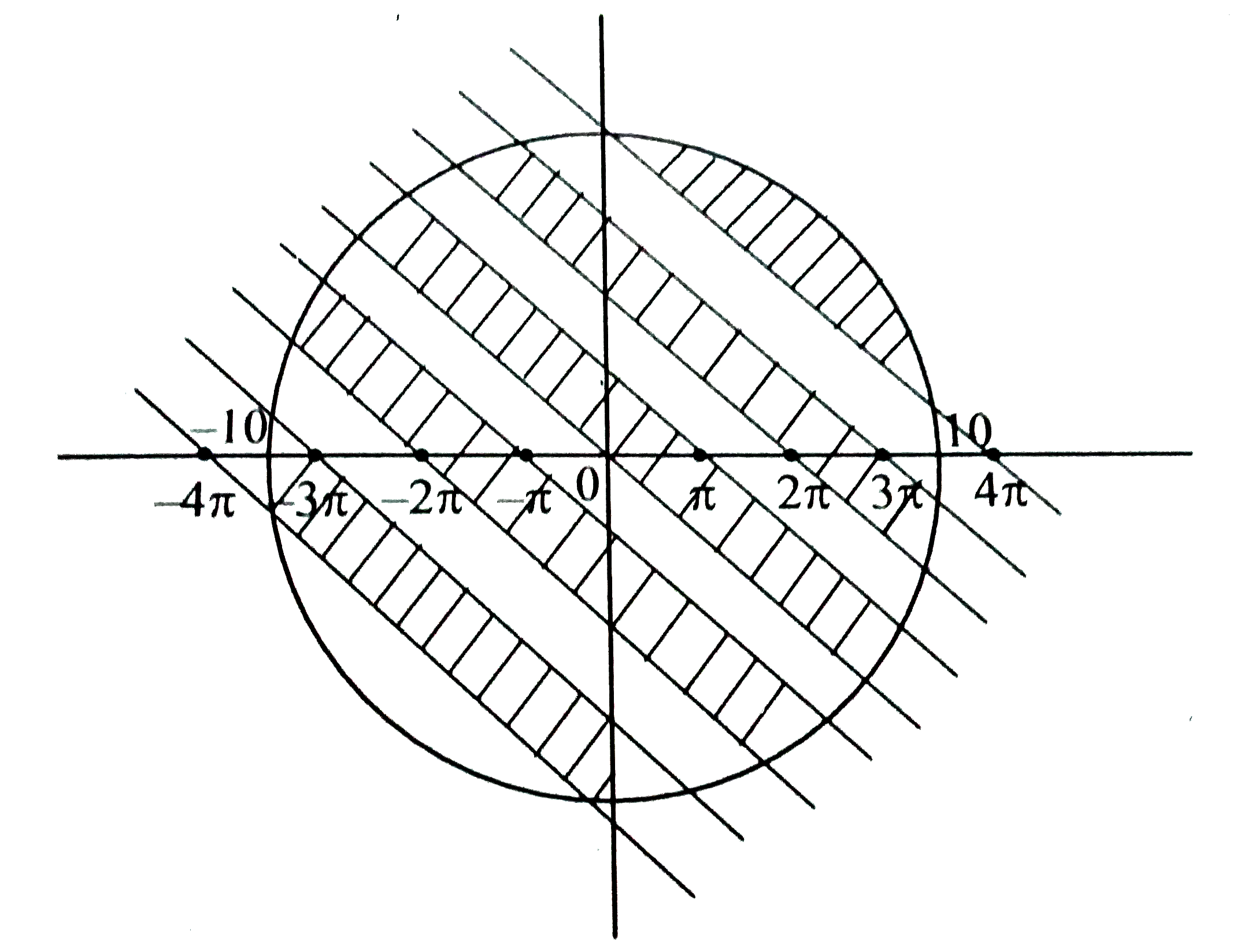
required area = shaded region $= \frac{1}{2} π {(10)}^{2} = 50 π$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider the regions $A = {(x, y) ∣ x^{2} + y^{2} \leq 100} and B = | \begin{matrix} x & y \end{matrix} | sin (x + y) > 0}$ in the plane. Then the area of the region $A \cap B$ is
A $10 π$
B100
C $100 π$
D $50 π$
Question 2 - Select One
The area of the region ${(x, y) : x^{2} + y^{2} \leq 1 \leq x + y}$ , is
A $\frac{π}{5}$
B $\frac{π}{4}$
C $\frac{π^{2}}{4}$
D $\frac{π}{4} - \frac{1}{2}$
Question 3 - Select One
The area of the region described by $A = {(x, y) : x^{2} + y^{2} \leq 1$ and $y^{2} \leq 1 - x}$ is :
A $\frac{π}{2} - \frac{2}{3}$
B $\frac{π}{2} + \frac{2}{3}$
C $\frac{π}{2} + \frac{4}{3}$
D $\frac{π}{2} + \frac{4}{3}$

KVPY PREVIOUS YEAR-KVPY-exercise

Home
Ask Doubt
Profile