A polynomial P(x) with real coefficients has the property that Pn(x)≠0 for all x. Suppose P(0)=1 and P'(0) = −1.
What can you say about P(1)?
P(1)≥0
P(1)≠0
P(1)≤0
−1/2<P(1)<1/2
The correct Answer is:C
P(x)=e−x P(0)=1
P'(x)=−e−x P'(0)=−1 P''(x)=e−x≠0∀x∈R
P(1)=1e
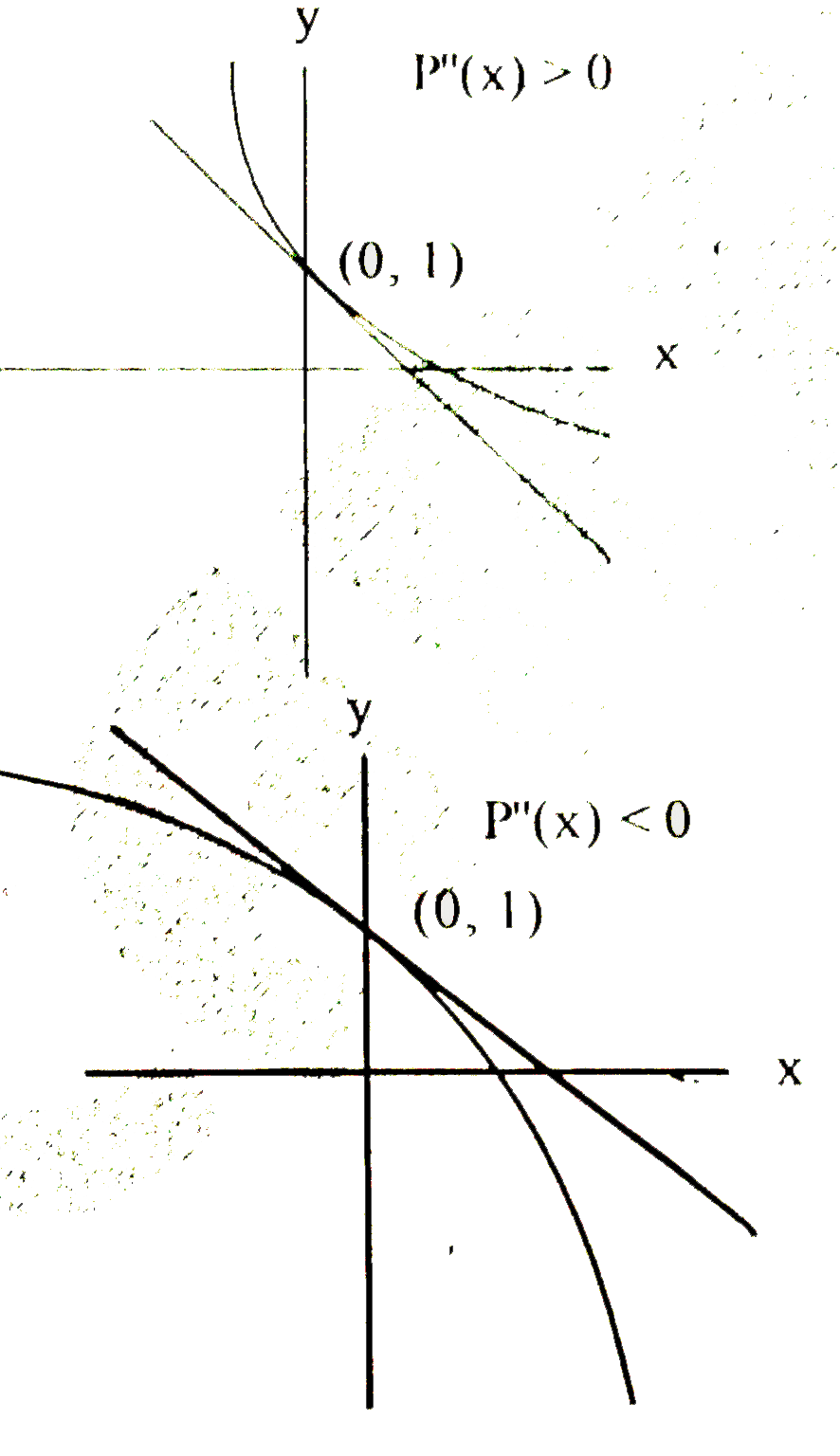
P(x)=−ex+2
P'(x)=−ex
P'(0)=−1
P''(x)=−e−x
P(1)=−e+2 P(1)≠0
=−0.7
Topper's Solved these Questions
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART -I MATHEMATICS
Explore 20 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-II MATHEMATICS
Explore 10 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-2 MATHEMATICS
Explore 5 Videos
- KVPY 2021Book:KVPY PREVIOUS YEARChapter:KVPY 2021Exercise:PART II MATHEMATICS
Explore 4 Videos
Similar Questions
Let P(x) be a quadratic polynomial with real coefficients such that for all real x the relation 2(1+P(x))=P(x−1)+P(x+1) holds. If P(0)=8 and P(2)=32, then Sum of all the coefficients of P(x) is:
View SolutionLet p (x) be a polynomial with real coefficient and p(x)=p'(x)=x2+2x+1. Find P (1).
View Solution
Knowledge Check
Let P(x) be quadratic polynomical with real coefficient such tht for all real x the relation 2(1+P(x))=P(x−1)+P(x+1) holds. If P(0)=8 and P(2)=32 then
Sum of all coefficients of P(x) can not beA20B19C17D15Let P(x) be a polynomial with real coefficients such that ∫10xmP(1−x)dx=0∀minN∪{0}, then
AP(x)=xn(1−x)n for some n∈NBP(x) = (1−x)2n for some n∈NCP(x) = 1−xm(1−x)n for some m, n∈NDP(x)=0Let P(x) be a polynomial of degree n with real coefficients and is non negative for all real x then P(x)+P1(x)+...+Pn(x) is
Anon negative for all xBnon positive for all xCmay be positive or negativeDcan't say
Question Number 2 Let P(x) be a polynomial with real coefficients such that P(sin2 ) P(cos2 x). for all re [0, π/2]. Consider the following statements: I. P(x) is an even function II. P(x) can be expressed as a polynomial in (2x - 1)2. III. P(x) is a polynomial of even degree Then Bonly I and II are tue D. all are true A. all are false C only II and III are true
View SolutionQuestion Number 2 Let P(x) be a polynomial with real coefficients such that P(sin2 ) P(cos2 x). for all re [0, π/2]. Consider the following statements: I. P(x) is an even function II. P(x) can be expressed as a polynomial in (2x - 1)2. III. P(x) is a polynomial of even degree Then Bonly I and II are tue D. all are true A. all are false C only II and III are true
View SolutionLet p(x) be a quadratic polynomial with real coefficient such that for all real x, the relation 2(−1+p(x))=p(x−1)+p(x+1) holds if p(0)=4,p(2)=16. 1) The sum of all coefficient of p(x) is 2) Coefficient of x is 3) If the range of p(x) is (−∞,m), then the value of m is
View SolutionLet P(x)=x2+12x+b and Q(x)=x2+cx+d be two polynomials with real coefficients such that P(x)Q(x)=Q(P(x)) for all real x. Find all the real roots of P(Q(x))=0.
View SolutionLet P(x)=x2+12x+b and Q(x)=x2+cx+d be two polynomials with real coefficients such that P(x)Q(x)=Q(P(x)) for all real x. Find all the real roots of P(Q(x)) =0.
View Solution
