Suppose OABC is a reatangle in the xy-plane where O is the origin and A, B lie on the parabola $y = x^{2}$ .Then C must lie on the curve

A

$y = x^{2} + 2$

B

$y = 2 x^{2} + 1$

C

$y = - x^{2} + 2$

D

$y = - 2 x^{2} + 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

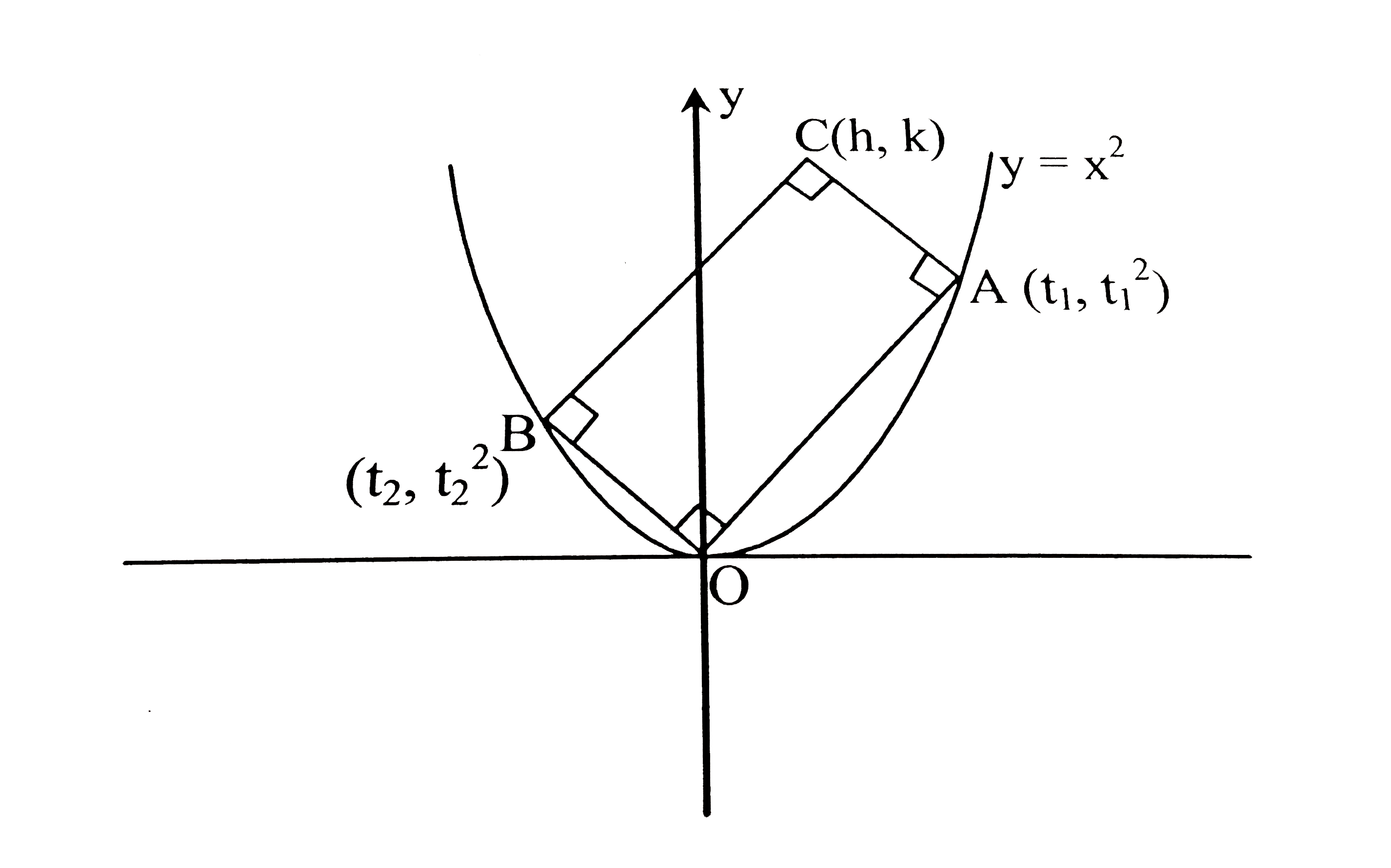
$∵ O B ⊥ O A$
$S o, t_{1} t_{2} = - 1$
$N o w \frac{h}{2} = \frac{t_{1} + t_{2}}{2}$
$t_{2} + t_{2} = h$ . . . (1)
$a l s o t_{1}^{2} + t_{2}^{2} = k$
${(t_{1} + t_{2})}_{1}^{2} - 2 t_{1} t_{2} = k$
$h^{2} + 2 = k$
locus is $x^{2} + 2 = y$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
Which of the following points lie on the parabola $x^{2} = 4 a y$
A $x = a t^{2}, y = 2 a t$
B $x = 2 a t, y = a t$
C $x = 2 a t^{2}, y = a t$
D $x = 2 a t, y = a t^{2}$
Question 2 - Select One
Tangents are drawn from the origin to the curve y=sin x then ,the point of contact lie on the curve is
A $y^{2} = \frac{x^{2}}{1 - x^{2}}$
B $y^{2} = \frac{x^{2}}{1 + y}$
C $x^{2} = \frac{y^{2}}{1 + y^{2}}$
D $y^{2} = \frac{x^{2}}{1 + x^{2}}$
Question 3 - Select One
The points of contact of the tangents drawn from the origin to the curve y = sin x lie on the curve
A $x^{2} - y^{2} = x y$
B $x^{2} + y^{2} = x^{2} y^{2}$
C $x^{2} - y^{2} = x^{2} y^{2}$
DNone of these

Recommended Questions

Home
Ask Doubt
Profile