Find the about the mean for the following data:
Marks
obtained , 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
Number of
students, 2, 3, 8, 14, 8, 3, 2
To find the mean deviation from the mean for the given data, we will follow these steps:
Step 1: Create a Frequency Table
We will create a table with the classes, mid-values (XI), frequencies (fi), and the product of frequency and mid-values (fi * XI).
| Marks Obtained | Mid-value (XI) | Frequency (fi) | fi * XI |
|----------------|----------------|----------------|---------|
| 10 - 20 | 15 | 2 | 30 |
| 20 - 30 | 25 | 3 | 75 |
| 30 - 40 | 35 | 8 | 280 |
| 40 - 50 | 45 | 14 | 630 |
| 50 - 60 | 55 | 8 | 440 |
| 60 - 70 | 65 | 3 | 195 |
| 70 - 80 | 75 | 2 | 150 |
| Total | | 40 | 1800|
Step 2: Calculate the Mean
To calculate the mean (X̄), we use the formula:
Xˉ=Σ(fi⋅XI)Σfi
Substituting the values:
Xˉ=180040=45
Step 3: Calculate the Deviation from the Mean
Next, we calculate the deviation (DI) of each mid-value from the mean (45):
| Mid-value (XI) | Deviation (DI = XI - X̄) |
|----------------|--------------------------|
| 15 | 15 - 45 = -30 |
| 25 | 25 - 45 = -20 |
| 35 | 35 - 45 = -10 |
| 45 | 45 - 45 = 0 |
| 55 | 55 - 45 = 10 |
| 65 | 65 - 45 = 20 |
| 75 | 75 - 45 = 30 |
Step 4: Calculate the Absolute Deviations
Now, we take the absolute values of the deviations:
| Mid-value (XI) | |DI| |
|----------------|----|
| 15 | 30 |
| 25 | 20 |
| 35 | 10 |
| 45 | 0 |
| 55 | 10 |
| 65 | 20 |
| 75 | 30 |
Step 5: Calculate fi * |DI|
Now we multiply each absolute deviation by the corresponding frequency:
| Frequency (fi) | |DI| | fi * |DI| |
|----------------|----|----|
| 2 | 30 | 60 |
| 3 | 20 | 60 |
| 8 | 10 | 80 |
| 14 | 0 | 0 |
| 8 | 10 | 80 |
| 3 | 20 | 60 |
| 2 | 30 | 60 |
| Total | | | 400 |
Step 6: Calculate the Mean Deviation
Finally, we calculate the mean deviation (MD) using the formula:
MD=Σ(fi⋅|DI|)Σfi
Substituting the values:
MD=40040=10
Final Result
The mean deviation from the mean for the given data is 10.
---
We will create a table with the classes, mid-values (XI), frequencies (fi), and the product of frequency and mid-values (fi * XI).
|----------------|----------------|----------------|---------|
| 10 - 20 | 15 | 2 | 30 |
| 20 - 30 | 25 | 3 | 75 |
| 30 - 40 | 35 | 8 | 280 |
| 40 - 50 | 45 | 14 | 630 |
| 50 - 60 | 55 | 8 | 440 |
| 60 - 70 | 65 | 3 | 195 |
| 70 - 80 | 75 | 2 | 150 |
| Total | | 40 | 1800|
To calculate the mean (X̄), we use the formula:
Next, we calculate the deviation (DI) of each mid-value from the mean (45):
|----------------|--------------------------|
| 15 | 15 - 45 = -30 |
| 25 | 25 - 45 = -20 |
| 35 | 35 - 45 = -10 |
| 45 | 45 - 45 = 0 |
| 55 | 55 - 45 = 10 |
| 65 | 65 - 45 = 20 |
| 75 | 75 - 45 = 30 |
Now, we take the absolute values of the deviations:
|----------------|----|
| 15 | 30 |
| 25 | 20 |
| 35 | 10 |
| 45 | 0 |
| 55 | 10 |
| 65 | 20 |
| 75 | 30 |
Now we multiply each absolute deviation by the corresponding frequency:
|----------------|----|----|
| 2 | 30 | 60 |
| 3 | 20 | 60 |
| 8 | 10 | 80 |
| 14 | 0 | 0 |
| 8 | 10 | 80 |
| 3 | 20 | 60 |
| 2 | 30 | 60 |
| Total | | | 400 |
Finally, we calculate the mean deviation (MD) using the formula:
The mean deviation from the mean for the given data is 10.
Similar Questions
Find the about the mean for the following data:
Marks obtained , 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
Number of students, 2, 3, 8, 14, 8, 3, 2
View SolutionObtain the mean , median and mode of the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 5 7 15 25 20 15 8 5
View SolutionFind the mean deviation about median for the following data
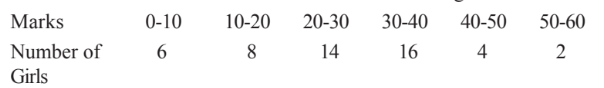
View SolutionCaculate the median and mode from the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 2 18 30 45 35 20 6 3
View SolutionFind the mean deviation from the mean of the following data:
Classes:, 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
freequency:2, 3, 8, 14, 8, 3, 2
View SolutionFind out median , with the help of the following data :
Price Level10−2020−3030−4040−5050−6060−70Number of Commodity 2 5 8 4 6 3
View SolutionCalculate mean from the following data:
Marks10−2010−3010−4010−5010−6010−7010−8010−90Number of Students 4 16 56 97 124 137 146 150
View SolutionCalculate mean from the following data:
Marks10−2010−3010−4010−5010−6010−7010−8010−90Number of Students 4 16 56 97 124 137 146 150
View SolutionCalculate the median deviation from the median of the following data: Wages per week (in Rs.), 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80 No. of workers, 4, 6, 10, 20, 10, 6, 4
View SolutionFind the median of the following data:
Class Interval0−1010−2020−3030−4040−50f68547
View Solution