Let f(x) is a continuous function on [−7,0] and differentiable function on the interval (−7,0) such that f(−7)=−3 and given that f'(c)≤2 for c∈(−7,0).If the largest possible value of f(0) is k .Then the value of k3 is
Step by step video & image solution for Let f(x) is a continuous function on [-7,0] and differentiable function on the interval (-7,0) such that f(-7)=-3 and given that f'(c)<=2 for c in(-7,0).If the largest possible value of f(0) is k .Then the value of (k)/(3) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Let f(x) be a differentiable function in the interval (0, 2) then the value of ∫20f(x)dx
Af(c) where c∈(0,2)B2f(c), where c∈(0,2)Cf'(c) where c∈(0,2)DNone of theseLet f(x) be a differentiable function in the interval (0,2) then the value of ∫20f(x) is
Af(c )for some c∈(0,2)B2f(c )for some c∈(0,2)Cf'(c )for some c∈(0,1)Dnone of theseLet f(x) be a differentiable function in the interval (0,2) , then the value of ∫20f(x)dx is :
Af( c) for some c∈(0,2)B2f (c ) for some c∈(0,2)Cf.(c ) for some c∈(0,1)Dnone of these
If f be a continuous function on [0,1], differentiable in (0,1) such that f(1)=0,then there exists some c∈(0,1) such that
View SolutionLet f(x), be a function which is continuous in closed interval [0, 1] and differentiable in open interval ] 0,1[. Show that ∃ a point c∈]0,1[ such that f'(c)=f(1)−f(0).
View SolutionLet f be any continuous function on [0, 2] and twice differentiable on (0, 2). If f(0) = 0, f(1) = 1 and f(2) = 2, then :
View SolutionA function f(x) is, continuous in the closed interval [0,1] and differentiable in the open interval [0,1] prove that f'(x1)=f(1)−f(0),0<x1<1
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
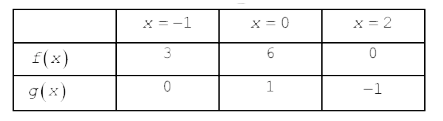
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View Solution