In an isosceles right angled triangle , a straight line drwan from the mid - point of one of equal sides to the opposite angle . It divides the angle into two parts , θand(π/4−θ) . Then tanθandtan[(π/4)−θ] are equal to
12,13
13,14
15,16
none of these
The correct Answer is:A
To solve the problem, we need to find the values of tanθ and tan(π4−θ) in the context of an isosceles right triangle where a line is drawn from the midpoint of one of the equal sides to the opposite angle.
1. Define the Triangle:
Let's denote the isosceles right triangle as △ABC where AB=AC=2x and ∠A=90∘. The midpoint of side AB is point G.
2. Draw the Line:
Draw a line from point G to point C. This line divides ∠A into two angles: θ and π4−θ.
3. Identify Triangle △ABG:
In triangle ABG:
- The length AG=x (since G is the midpoint of AB).
- The length BG=x (since G is the midpoint of AB).
- The length AB=2x.
4. Calculate tanθ:
Using the definition of tangent in triangle ABG:
tanθ=oppositeadjacent=AGBG=xx=1
However, we need to find the relationship involving 2x and x:
tanθ=2xx=2(using the full length of the side)
5. Calculate tan(π4−θ):
We use the identity:
tan(π4−θ)=1−tanθ1+tanθ
Substituting tanθ=2:
tan(π4−θ)=1−21+2=−13=−13
6. Final Values:
Thus, we have:
tanθ=2andtan(π4−θ)=−13
Conclusion:
The values of tanθ and tan(π4−θ) are 2 and −13 respectively.
Let's denote the isosceles right triangle as △ABC where AB=AC=2x and ∠A=90∘. The midpoint of side AB is point G.
Draw a line from point G to point C. This line divides ∠A into two angles: θ and π4−θ.
In triangle ABG:
- The length AG=x (since G is the midpoint of AB).
- The length BG=x (since G is the midpoint of AB).
- The length AB=2x.
Using the definition of tangent in triangle ABG:
tanθ=oppositeadjacent=AGBG=xx=1
However, we need to find the relationship involving 2x and x:
tanθ=2xx=2(using the full length of the side)
We use the identity:
tan(π4−θ)=1−tanθ1+tanθ
Substituting tanθ=2:
tan(π4−θ)=1−21+2=−13=−13
Thus, we have:
tanθ=2andtan(π4−θ)=−13
The values of tanθ and tan(π4−θ) are 2 and −13 respectively.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II20videos
STRAIGHT LINE
- BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - COMPREHENSIONS9videos
STRAIGHT LINE
- BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II14videos
STRAIGHT LINE
- BOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Comprehension Type6videos
STATISTICS
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS328videos
TEST PAPERS
Similar Questions
Knowledge Check
- Question 1 - Select One
tan(π4+θ)tan(3π4+θ) is equal to
A−2B−1C1D0 - Question 2 - Select One
tan(π4+θ)−tan(π4−θ)=
A2tan2θB2cot2θCtan2θDcot2θ - Question 3 - Select One
ABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , tanθtanϕ =
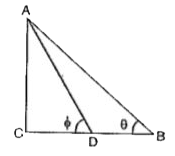 A1B1√2C12D2
A1B1√2C12D2
If tanθ=−43 then sinθ is equal to
View SolutionIf tanθ+tan(π3+θ)+tan(2π3+θ)=ktan3θ then k is equal to
View SolutionIftanθ+tan4θ+tan7θ=tanθtan4θtan7θ, thenθ is equal to
View SolutionIf 0<θ<π/4 and tanθ=4/5, then tan2θ+sec2θ is equal to ________
View Solutiontan(π4+θ2)+tan(π4−θ2) is equal to
View Solution

