The locus of the point (√3h,√√3k+2) if it lies on the line x−y−1=0 is straight line (b) a circle a parabola (d) none of these
Straight line
Circle
Parabola
None of these
The correct Answer is:C
Step by step video & text solution for The locus of the point (sqrt(3h),sqrt(sqrt(3)k+2)) if it lies on the line x-y-1=0 is straight line (b) a circle a parabola (d) none of these by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - PARABOLAEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE LEVEL - II)20videos
PARABOLA
- BOOK - FIITJEECHAPTER - PARABOLAEXERCISE - COMPREHENSIONS9videos
PARABOLA
- BOOK - FIITJEECHAPTER - PARABOLAEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE LEVEL - II)15videos
PARABOLA
- BOOK - FIITJEECHAPTER - MATRICES EXERCISE - NUMERICAL BASED3videos
MATRICES
- BOOK - FIITJEECHAPTER - PERMUTATIONS & COMBINATIONSEXERCISE - NUMERICAL BASED3videos
PERMUTATIONS & COMBINATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph of straight line y=√3x+2√3 is :
A B
B C
C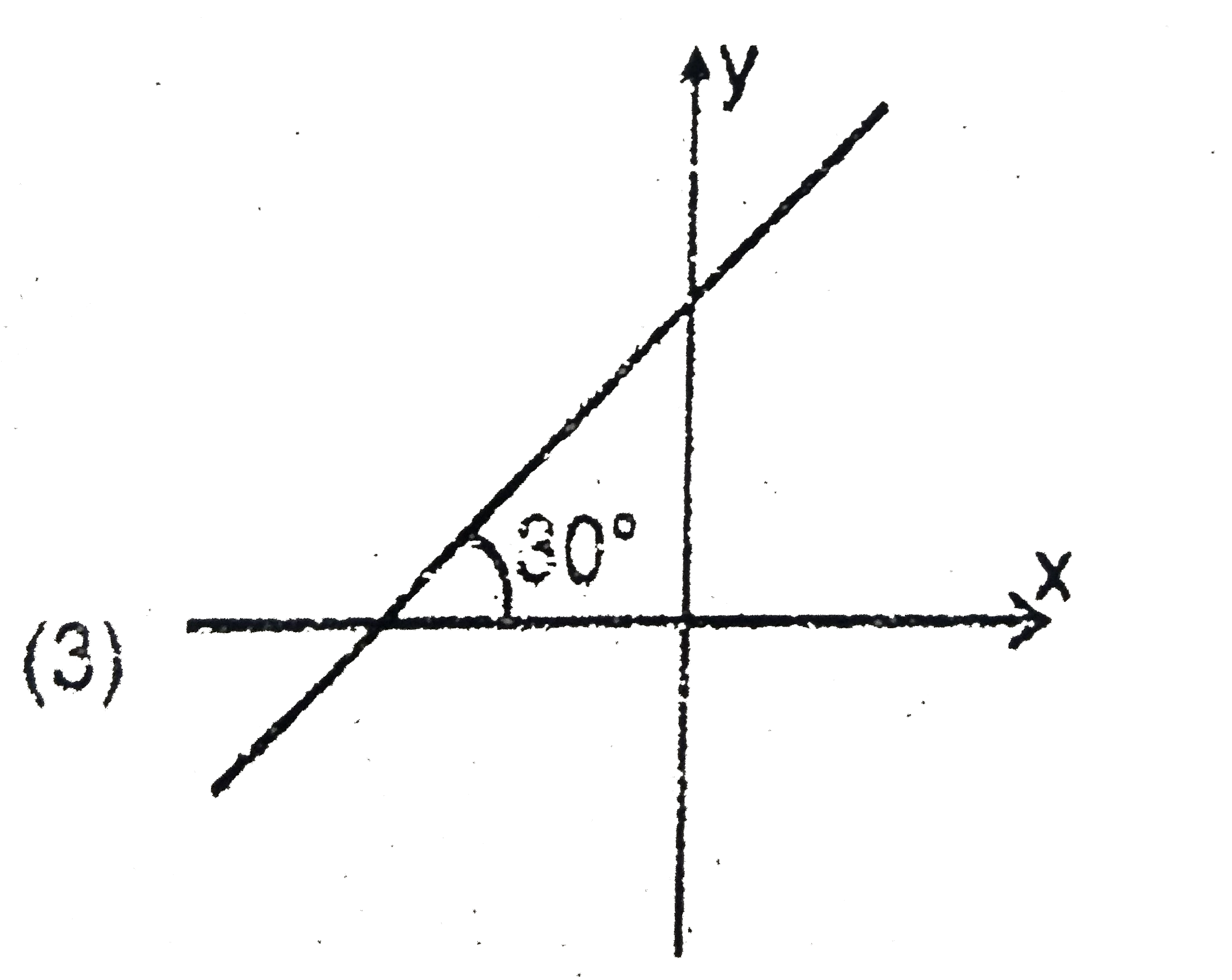 D
D
Distance of origin from the line (1+√3)y+(1−√3)x=10 along the line y=√3x+k (1) 2√5 (2) 5√2+k (3) 10 (4) 5
View SolutionIf xα+yβ=1 touches the circle x2+y2=a2 then point (1α,1β) lies on (a) straight line (b) circle (c) parabola (d) ellipse
View SolutionIf a ΔABC remains always similar to a given triangle and the point A is fixed and the point B always moves on a given straight line, then locus of C is (A) a circle (B) a straight line (C) a parabola (D) none of these
View SolutionThe equation √x2+4y2−4xy+4+x−2y=1 represent a (A) straight line (B) circle (C) parabola (D) pair of lines
View SolutionLocus of the image of the point (2, 3) in the line (2x−3y+4)+k(x−2y+3)=0,kεR , is a : (1) straight line parallel to x-axis. (2) straight line parallel to y-axis (3) circle of radius √2 (4) circle of radius √3
View SolutionThe locus of the point of intersection of the lines √3x−y−4√3t=0&√3tx+ty−4√3=0 (where t is a parameter) is a hyperbola whose eccentricity is:
View SolutionProve that the locus of the point of intersection of the lines √3x−y−4√3k=0and√3kx+ky−4√3=0 for different values of k is a hyperbola whose eccentricity is 2.
View Solution

