Points A(a) and B (b) are on xy=1, Circles with OA and OB as diameter, where O is the origin are drawn to intersect at p , then OP intersects the curve at
(1√ab,√ab)
(−1√ab,−√ab)
(√ab,1√ab)
all of these
The correct Answer is:A, B
Step by step video, text & image solution for Points A(a) and B (b) are on xy = 1 , Circles with OA and OB as diameter, where O is the origin are drawn to intersect at p , then OP intersects the curve at by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - FIITJEECHAPTER - HYPERBOLAEXERCISE - COMPREHENSIONS
9 Videos
- HYPERBOLABOOK - FIITJEECHAPTER - HYPERBOLAEXERCISE - MATCH THE COLUMN
6 Videos
- HYPERBOLABOOK - FIITJEECHAPTER - HYPERBOLAEXERCISE - ASSIGNMENT PROBLEMS ( OBJECTIVE) Level - I
47 Videos
- HEIGHTS & DISTANCE BOOK - FIITJEECHAPTER - HEIGHTS & DISTANCE EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II
20 Videos
- INDEFINTE INTEGRALBOOK - FIITJEECHAPTER - INDEFINTE INTEGRALEXERCISE - EXERCISE-8
1 Videos
Similar Questions
Knowledge Check
Two points A and B in a plane are related if OA = OB, where O is a fixed point. This relation is
Apartial order relationBequivalence relationCreflexive but not symmetricDreflexive but not transitiveOn the circle with centre O, points A, B are such that OA =AB. A point C is located on the tangent at B to the circle such that A and C are on the opposite sides of the line OB and Ab =BC. The line segment AC intersects the circle again at F. Then the ratio ∠BOF:∠BOC is equal to-
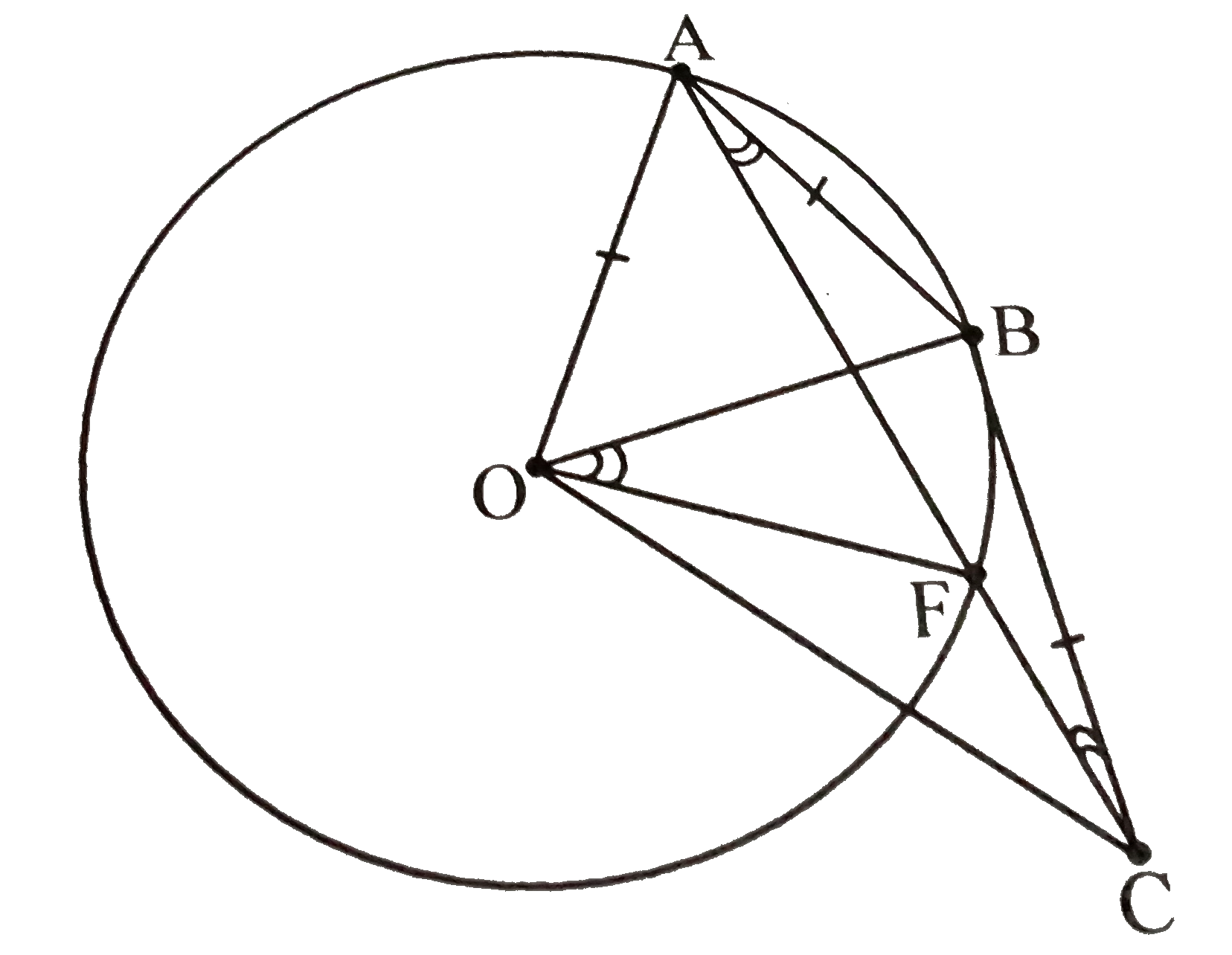 A1:2B2:3C3:4D4:5
A1:2B2:3C3:4D4:5A circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of 65∘ at any point C on the circumference of the circle. If P is the point of intersection for the two lines, then the measure of ∠APO is :
A25∘B65∘C90∘D40∘
Two circles are drawn as OA and OB as diameters,where O is origin,A is (-4,6) and B is (8,4) .Then the length of common chord of the circles is a√b where b-a equals
View SolutionA circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of 65∘ at any point C on the circumference of the circle. If P is the point of intersection for the two lines, then the measure of ∠APO is :
View SolutionP is a point outside a circle with centre O, and it is 14 cm away from the centre. A secant PAB drawn from P intersects the circle at the points A and B such that PA = 10 cm and PB = 16 cm. The diameter of the Circle is:
View SolutionIf two points A and B lie on the curve y=x2 such that −−→OA.ˆi=1and−−→OB.ˆj=4, where O is origin and A and B lie in the 1st and 2nd quadrant respectively, then −−→OA.−−→OB is equal to
View SolutionA curve in the first quadrant is such that the slope of OP is twice the slope of the tangent drawn at P to the curve, where O is the origin and P is any general point on the curve. If the curve passes through (4, 2), then its equation is
View Solution
