IF a function is symmetric about the x =2 and x = 3, then the functions are
all periodic functions with fundametnal period 3
all periodic functions with fundametnal period 2
all periodic functions with fundametnal period 1
none of these
The correct Answer is:C
To determine the functions that are symmetric about the lines x=2 and x=3, we can follow these steps:
Step 1: Understanding Symmetry
A function f(x) is symmetric about a vertical line x=a if it satisfies the condition:
f(a−d)=f(a+d)
for all values of d. This means that the function's values at equal distances from the line of symmetry are the same.
Step 2: Applying Symmetry Conditions
Given that the function is symmetric about both x=2 and x=3, we can set up the following equations based on the symmetry conditions:
1. For symmetry about x=2:
f(2−d)=f(2+d)
2. For symmetry about x=3:
f(3−d)=f(3+d)
Step 3: Finding a General Form
To find a function that satisfies both conditions, we can express the function in terms of periodic functions. A periodic function has the property that it repeats its values at regular intervals.
Step 4: Periodicity
If we consider a periodic function with a period that accommodates both lines of symmetry, we can use a function such as:
f(x)=f(2+k) and f(x)=f(3+k)
where k is a constant that defines the periodicity.
Step 5: Example Functions
A simple example of such a function could be:
f(x)=sin(π(x−2))
This function is periodic with a period of 2, which means it will repeat its values around both lines of symmetry.
Conclusion
Thus, the functions that are symmetric about x=2 and x=3 can be represented as periodic functions, such as:
f(x)=sin(π(x−2))
or any other function that satisfies the periodicity condition.
A function f(x) is symmetric about a vertical line x=a if it satisfies the condition:
f(a−d)=f(a+d)
for all values of d. This means that the function's values at equal distances from the line of symmetry are the same.
Given that the function is symmetric about both x=2 and x=3, we can set up the following equations based on the symmetry conditions:
f(2−d)=f(2+d)
f(3−d)=f(3+d)
To find a function that satisfies both conditions, we can express the function in terms of periodic functions. A periodic function has the property that it repeats its values at regular intervals.
If we consider a periodic function with a period that accommodates both lines of symmetry, we can use a function such as:
f(x)=f(2+k) and f(x)=f(3+k)
where k is a constant that defines the periodicity.
A simple example of such a function could be:
f(x)=sin(π(x−2))
This function is periodic with a period of 2, which means it will repeat its values around both lines of symmetry.
Thus, the functions that are symmetric about x=2 and x=3 can be represented as periodic functions, such as:
f(x)=sin(π(x−2))
or any other function that satisfies the periodicity condition.
Topper's Solved these Questions
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - ASSERTION REASONING
8 Videos
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - MCQ (MULTIPLE CORRECT)
37 Videos
- TIPSBOOK - FIITJEECHAPTER - TIPSEXERCISE - ASSIGNMENT (SECTION (I): MCQ (SINGLE CORRECT)
125 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
328 Videos
- TRIGNOMETRIC RATIOS AND IDENTITIESBOOK - FIITJEECHAPTER - TRIGNOMETRIC RATIOS AND IDENTITIESEXERCISE - All Questions
1 Videos
Similar Questions
Which of the following statement is/are always true concerning the function f(x)=x+1x (I)The graph of the function is symmetric about the y-axis. (II)The graph of the function has a relatively maximum at (1, 2) and a relative minimum at (−1, −2). (III)The graph of the function is concave up for x>0 and concave down for x<0. (a)only I (b) only II (c)only III (d) only I and II
View Solutiony = f(x) be a real valued function with domain as all real numbers. If the graph of the function is symmetrical about the line x = 1, then for all α∈R
View Solution
Knowledge Check
If the function f(x) is symmetric about the line x=3, then the value of the integral I=∫8−2f(x)f(x)+f(6−x)dx is
A0B5C10D16If the graph of a function f(x is symmetrical about the line x = a, then
Af(a+x)=f(a−x)Bf(a+x)=f(x−a)Cf(x)=f(−x)Dnone of theseStatement 1: The function f (x) = sin x is symmetric about the line x = 0.
Statement 2: Every even function is symmetric about y-axis.AStatement-1 is True, Statement-2 is True and Statement-2 is a correct explanation for Statement-1BStatement-1 is True, Statement-2 is True and Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is True
83. A non-zero function f (x) is symmetrical about the line y=x then the value of λ (constant) such that f2(x)=(f−1(x))2−λxf(x)f−1(x)+3x2f(x) where all x∈R+
View SolutionIf the graph of the function
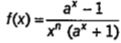 is symmetric about y-axis, then n is equal to :
is symmetric about y-axis, then n is equal to :
View SolutionA function whose graph is symmetric about y-axis is
View SolutionThe graph of the function y=f(x) is symmetrical about the line x=2, then :
View SolutionIf the garph of the function f(x)=ax3+x2+bx+c is symmetric about the line x = 2, then the value of a+b is equal to
View Solution
