A square ABCD of diagonal length 2a, is folded along the diagonal AC so that the planes DAC, BAC are at right angles. The shortest distance between DC and AB is
a√3
2a√3
√3a
none of these
The correct Answer is:B
Step by step video, text & image solution for A square ABCD of diagonal length 2a, is folded along the diagonal AC so that the planes DAC, BAC are at right angles. The shortest distance between DC and AB is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - ASSIGNMENT -OBJECTIVE84videos
MATHEMATICS TIPS
- BOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - ASSERTION - REASONING8videos
MATHEMATICS TIPS
- BOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - NUMERICAL DECIMAL BASED QUESTIONS21videos
MATHEMATICS TIPS
- BOOK - FIITJEECHAPTER - MATHEMATICS EXERCISE - NUMERICAL DECIMAL BASED QUESTIONS15videos
MATHEMATICS
- BOOK - FIITJEECHAPTER - MATRICES EXERCISE - NUMERICAL BASED3videos
MATRICES
Similar Questions
Knowledge Check
- Question 1 - Select One
A square ABCD of diagonal length 2a, is folded along the diagonal AC so that the planes DAC, BAC are at right angles. The shortest distance between DC and AB is
A√2aB2a/√3C2a/√5DNone - Question 2 - Select One
In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2) - Question 3 - Select One
In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)
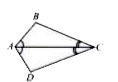
In the figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
 View Solution
View SolutionWhich of the following statements are true for a square? It is a rectangle. It has all its sides of equal length. Its diagonals bisect each other at a right angle. Its diagonals are equal to its sides.
View SolutionIf the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
View SolutionIf the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
View SolutionThree statements are given below:
I. In a rectangle ABCD, the diagonal AC bisects ∠A as well as ∠C.
II. In a square ABCD, the diagonal AC bisects ∠A as well as ∠C.
III. In a rhombus ABCD, the diagonal AC bisects ∠A as well as ∠C.
Which is true?View Solution

