The number of ways in which an examiner can assign 40 marks to 6 questions, giving not less than 3 marks to any question, is
27C22
27C21
26C22
none of these
The correct Answer is:A
To solve the problem of assigning 40 marks to 6 questions with the condition that each question receives at least 3 marks, we can follow these steps:
Step 1: Adjust the Marks
Since each of the 6 questions must receive at least 3 marks, we first allocate 3 marks to each question. This means we will initially distribute:
3×6=18 marks
Thus, we have:
40−18=22 marks left to distribute
Step 2: Define the New Variables
Let mi be the marks assigned to question i (where i=1,2,3,4,5,6). After assigning the minimum marks, we can redefine the marks for each question as:
m′i=mi−3
This means m′i can be zero or more (i.e., m′i≥0). The equation now becomes:
m′1+m′2+m′3+m′4+m′5+m′6=22
Step 3: Use the Stars and Bars Theorem
Now, we need to find the number of non-negative integer solutions to the equation:
m′1+m′2+m′3+m′4+m′5+m′6=22
According to the stars and bars theorem, the number of ways to distribute n indistinguishable objects (marks) into r distinguishable boxes (questions) is given by:
(n+r−1r−1)
In our case, n=22 and r=6:
Number of ways=(22+6−16−1)=(275)
Step 4: Calculate the Binomial Coefficient
Now we compute:
(275)=27!5!(27−5)!=27!5!⋅22!
Calculating this gives:
(275)=27×26×25×24×235×4×3×2×1=142506
Final Answer
Thus, the number of ways in which an examiner can assign 40 marks to 6 questions, giving not less than 3 marks to any question, is:
142506
Since each of the 6 questions must receive at least 3 marks, we first allocate 3 marks to each question. This means we will initially distribute:
3×6=18 marks
Thus, we have:
40−18=22 marks left to distribute
Let mi be the marks assigned to question i (where i=1,2,3,4,5,6). After assigning the minimum marks, we can redefine the marks for each question as:
m′i=mi−3
This means m′i can be zero or more (i.e., m′i≥0). The equation now becomes:
m′1+m′2+m′3+m′4+m′5+m′6=22
Now, we need to find the number of non-negative integer solutions to the equation:
m′1+m′2+m′3+m′4+m′5+m′6=22
According to the stars and bars theorem, the number of ways to distribute n indistinguishable objects (marks) into r distinguishable boxes (questions) is given by:
(n+r−1r−1)
In our case, n=22 and r=6:
Number of ways=(22+6−16−1)=(275)
Now we compute:
(275)=27!5!(27−5)!=27!5!⋅22!
Calculating this gives:
(275)=27×26×25×24×235×4×3×2×1=142506
Thus, the number of ways in which an examiner can assign 40 marks to 6 questions, giving not less than 3 marks to any question, is:
142506
Topper's Solved these Questions
- MATHEMATICS TIPSBOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - ASSERTION - REASONING
8 Videos
- MATHEMATICS TIPSBOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - MCQ (MULTIPLE CORRECT)
30 Videos
- MATHEMATICS TIPSBOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - ASSIGNMENT (SECTION (I) : MCQ (SINGLE CORRECT)
120 Videos
- MATHEMATICS BOOK - FIITJEECHAPTER - MATHEMATICS EXERCISE - NUMERICAL DECIMAL BASED QUESTIONS
15 Videos
- MATRICES BOOK - FIITJEECHAPTER - MATRICES EXERCISE - NUMERICAL BASED
3 Videos
Similar Questions
Knowledge Check
If 75% of a number is added to 75, then the result is the number itself. The number is:
Aa. 50Bb. 60Cc. 300Dd. 400The number of ways in which an examiner can assign 50 marks to 10 questions giving not less than 3 marks to any question is :
A29C9B47C3C52C2D40C10In how many ways in which an examiner can assign 30 marks to 8 questions, giving not less than 2 marks to any question.
A11B21C7C18D235
The given graph shows the marks obtained by students in an examination
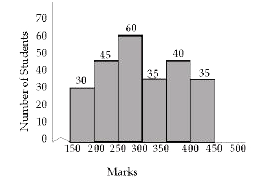
The number of students who obtained less than 300 marks is what percent more than the number of students who obtained 350 or more marks
View SolutionThe given graph shows the marks obtained by students in an examination.
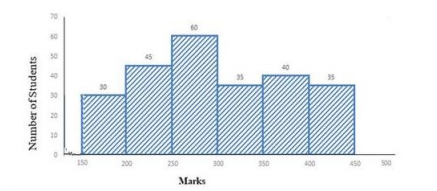 The number of students who obtained less than 300 marks is what percent more than the number of students who obtained 350 or more marks?
The number of students who obtained less than 300 marks is what percent more than the number of students who obtained 350 or more marks?
View SolutionThe number of ways in which an examiner can assign 30 marks to 8 questions, giving not less than 2 marks to any question is :
View SolutionThe number of ways in which an examiner can assign 30 marks to 8 question, giving no less than 2 marks to any question is :
View SolutionThe number of different ways of assigning 10 marks among 3 questions , each carrying at least 1 mark
View Solution
