The remainder when (2345)676+(1234)567 is divided by 4 is _____________
The correct Answer is:1
To find the remainder when (2345)676+(1234)567 is divided by 4, we can simplify the problem using modular arithmetic.
1. Find 2345mod4:
2345÷4=586(quotient)
2345−(586×4)=2345−2344=1
Thus, 2345≡1mod4.
2. Find (2345)676mod4:
Since 2345≡1mod4:
(2345)676≡1676≡1mod4
3. Find 1234mod4:
1234÷4=308(quotient)
1234−(308×4)=1234−1232=2
Thus, 1234≡2mod4.
4. Find (1234)567mod4:
Since 1234≡2mod4:
(1234)567≡2567mod4
We know that:
- 21≡2mod4
- 22≡0mod4
- For any n≥2, 2n≡0mod4.
Since 567≥2:
2567≡0mod4
5. Combine results:
Now we can combine the results:
(2345)676+(1234)567≡1+0≡1mod4
Thus, the remainder when (2345)676+(1234)567 is divided by 4 is 1.
2345÷4=586(quotient)
2345−(586×4)=2345−2344=1
Thus, 2345≡1mod4.
Since 2345≡1mod4:
(2345)676≡1676≡1mod4
1234÷4=308(quotient)
1234−(308×4)=1234−1232=2
Thus, 1234≡2mod4.
Since 1234≡2mod4:
(1234)567≡2567mod4
We know that:
- 21≡2mod4
- 22≡0mod4
- For any n≥2, 2n≡0mod4.
2567≡0mod4
Now we can combine the results:
(2345)676+(1234)567≡1+0≡1mod4
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - NUMERICAL DECIMAL BASED QUESTIONS21videos
MATHEMATICS TIPS
- BOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - PARAGRAPH BASED (MULTIPLE CHOICE) (COMPERHENSION - XVI)3videos
MATHEMATICS TIPS
- BOOK - FIITJEECHAPTER - MATHEMATICS EXERCISE - NUMERICAL DECIMAL BASED QUESTIONS15videos
MATHEMATICS
- BOOK - FIITJEECHAPTER - MATRICES EXERCISE - NUMERICAL BASED3videos
MATRICES
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the remainder when 41000 is divided by 7 ?
A1B4C2D6 - Question 2 - Select One
The remainder when 54n is divided by 13, is
A1B8C9D10
What is the remainder when 41012 is divided by 7 ?
View SolutionFind the remainder when 123×1234 is divided by 15.
View SolutionWhat is the remainder when 41000 is divided by 7?
View SolutionThe remainder when 54n is divided by 13, is
View SolutionWhen N is divided by 4, the remainder is 3. What is the remainder when 2N is divided by 4?
View SolutionRemainder when
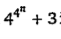 is divided by 7 is:View Solution
is divided by 7 is:View Solution

