Problems in which shape of figures is changed
To solve the problem of changing the shape of figures, we will follow a systematic approach. Let's take the two examples discussed in the video transcript and break them down step by step.
Example 1: Wire of Length 440 Meters
Step 1: Understand the Problem
We have a wire of length 440 meters that is modulated into the shape of a circle and then a square.
Step 2: Calculate the Radius of the Circle
The length of the wire when shaped into a circle becomes the circumference of the circle.
- Circumference C=2πr
- Set C=440 meters
- Therefore, 440=2×227×r
Step 3: Solve for Radius r
r=440×72×22=70 meters
Step 4: Calculate the Side of the Square
When the wire is shaped into a square, the length of the wire becomes the perimeter of the square.
- Perimeter P=4a
- Set P=440 meters
- Therefore, 440=4a
Step 5: Solve for Side a
a=4404=110 meters
Step 6: Calculate the Areas
- Area of the Circle Ac=πr2=227×(70)2=15400 m2
- Area of the Square As=a2=(110)2=12100 m2
Step 7: Find the Ratio of Areas
Ratio=AcAs=1540012100=1411
Example 2: Circular Wire of Diameter 42 cm
Step 1: Understand the Problem
A circular wire of diameter 42 cm is bent into the shape of a rectangle, with the sides in the ratio 6:5.
Step 2: Calculate the Radius of the Circle
- Diameter = 42 cm, so Radius r=422=21 cm
Step 3: Calculate the Circumference
- Circumference C=2πr=2×227×21=132 cm
Step 4: Set Up the Perimeter of the Rectangle
Let the length be 6x and the breadth be 5x.
- Perimeter P=2(l+b)=2(6x+5x)=22x
Step 5: Set the Perimeter Equal to the Circumference
22x=132
Step 6: Solve for x
x=13222=6
Step 7: Calculate Length and Breadth
- Length l=6x=6×6=36 cm
- Breadth b=5x=5×6=30 cm
Step 8: Calculate the Area of the Rectangle
Area=l×b=36×30=1080 cm2
Final Answers
1. The ratio of the areas of the circle and square is 1411.
2. The area of the rectangle formed from the circular wire is 1080 cm2.
We have a wire of length 440 meters that is modulated into the shape of a circle and then a square.
The length of the wire when shaped into a circle becomes the circumference of the circle.
- Circumference C=2πr
- Set C=440 meters
- Therefore, 440=2×227×r
r=440×72×22=70 meters
When the wire is shaped into a square, the length of the wire becomes the perimeter of the square.
- Perimeter P=4a
- Set P=440 meters
- Therefore, 440=4a
a=4404=110 meters
- Area of the Circle Ac=πr2=227×(70)2=15400 m2
- Area of the Square As=a2=(110)2=12100 m2
Ratio=AcAs=1540012100=1411
A circular wire of diameter 42 cm is bent into the shape of a rectangle, with the sides in the ratio 6:5.
- Diameter = 42 cm, so Radius r=422=21 cm
- Circumference C=2πr=2×227×21=132 cm
Let the length be 6x and the breadth be 5x.
- Perimeter P=2(l+b)=2(6x+5x)=22x
22x=132
x=13222=6
- Length l=6x=6×6=36 cm
- Breadth b=5x=5×6=30 cm
Area=l×b=36×30=1080 cm2
1. The ratio of the areas of the circle and square is 1411.
2. The area of the rectangle formed from the circular wire is 1080 cm2.
Similar Questions
Knowledge Check
- Question 1 - Select One
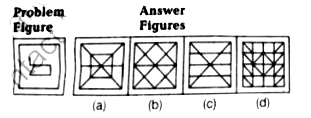
Choose the option figure in which the problem figure is hidden/embedded.
Figure
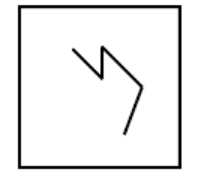 A
A
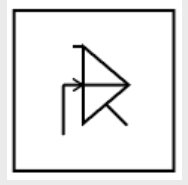 B
B
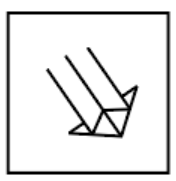 C
C
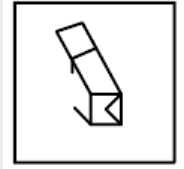 D
D

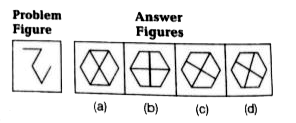
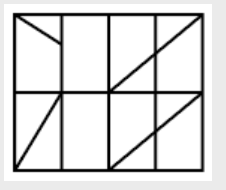
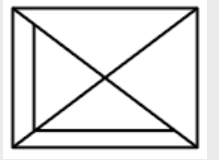
- Question 2 - Select One
Choose the option figure in which the problem figure is hidden/embedded.
Figure
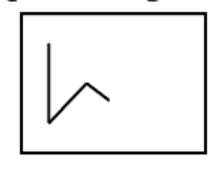 A
A
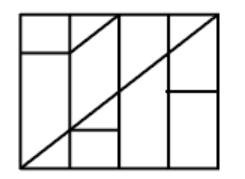 B
B
 C
C
 D
D

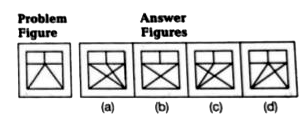
In the following problems from the given answer figure , select the one in which the problems figure is hidden embedded.
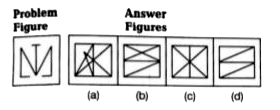 View Solution
View SolutionIn the following problems from the given answer figure , select the one in which the problems figure is hidden embedded.
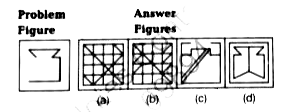 View Solution
View SolutionIn the following problems from the given answer figure , select the one in which the problems figure is hidden embedded.
 View Solution
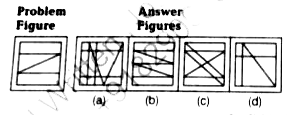
View SolutionIn the following problems from the given answer figure , select the one in which the problems figure is hidden embedded.
 View Solution
View SolutionIn the following problems from the given answer figure , select the one in which the problems figure is hidden embedded.
 View Solution
View SolutionIn the following problems from the given answer figure , select the one in which the problems figure is hidden embedded.
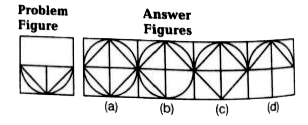 View Solution
View Solution