Combinations
Combinations
In Mathematics, the concept combination is very crucial. To represent a group of objects by selecting them in a set and also forming a subset is known as permutations and combinations. You should know how to deal with the different types of permutations and combinations problem in the right way. We will have a look at the various permutations and combinations questions that would help in getting the perfect idea about it. When objects or data are selected from a certain group, it is known as permutations and on the other hand the representation which is made in order is called combination.
What is Combination?
When an item is selected from a collection such that it does not matter when it comes to the order of selection, then it is known as combination. When repetition is allowed, the terms k-combination or k-selection are often used.
Formulas
When it comes to the formula involving permutation and combination concept, there are two key formulas are:
Permutation Formula
A permutation is the choice of r things from a set of n things which is without replacement and where the order matters.
nPr = (n!) / (n-r)!
Combination Formula
A combination happens to be the choice of r things from a set of n things which is without replacement and where order does not matter.
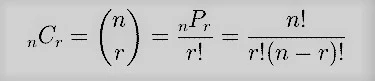
Differences between Permutation and Combination
Permutation
Combination
It consists of the arrangement of numbers, people, digits, letters, colours, and alphabets,
It consists of the selection of food, clothes menu, subjects, team.
Picking of a pitcher, team captain and shortstop from a group.
Picking of three team members from a group.
Picking of two favourite colours, in order, from a colour brochure.
Picking of two colours from a colour brochure.
Picking the first, second and third place winners.
Picking the three winners.
Related Videos:
- Factorial: definition and notation
- Problems based on factorial
- Problems based on finding the no of arrangement of letters of the given word
- Problems based on selection of certain no of people from a given no of people
Let us try to work on some permutations and combinations questions that would help in finding the right way as to how to solve it without any difficulties.
Question 1: There is a group of 6 boys and 4 girls. Here, you need to select four children. Can you calculate as to how many different ways can they be selected such that at least one boy should be there?
A. 212 B. 134
C. 209 D. 201
Solution: Here, we have got 4 options as given below
4 boys can be selected ...(option 1)
The number of ways to this = 6C4
3 boys and 1 girl can be selected ...(option 2)
The number of ways to this = 6C3 × 4C1
2 boys and 2 girls can be selected ...(option 3)
The number of ways to this = 6C2 × 4C2
1 boy and 3 girls can be selected ...(option 4)
The number of ways to this = 6C1 × 4C3
So, the total number of ways
= 6C4 + 6C3 × 4C1 + 6C2 × 4C2 + 6C1 × 4C3
= 6C2 + 6C3 × 4C1 + 6C2 × 4C2 + 6C1 × 4C1[∵ nCr = nC(n-r)]
=6 × 52 × 1 + 6 × 5 × 43 × 2 × 1 × 4 = 6 × 52 × 1 + 6 × 5 × 43 × 2 × 1 × 4 + 6× 52 × 1 × 4× 32 ×1 + 6 × 4 + 6 × 52 × 1 × 4 × 32 × 1 + 6 × 4
So, we get =15 + 80 + 90 + 24 = 209
The answer is Option C.
Question 2: Determine the number of ways for the letters of the word 'OPTICAL' can be arranged so that the vowels always come together?
A. 720 B. 825
C. 920 D. 610
Solution: There are 7 letters in the word, “OPTICAL”. There are 3 vowels which are ‘O’, ‘I’, and ‘A’ where it always comes together. So, we can say that grouping can be done for these 3 vowels where it can be considered as a single letter, i.e. PTCL (OIA).
So, it can be assumed that the total letters as 5 where we can find that all these letters are different.
Therefore, the number of ways by which the letters can be arranged is:
5! = 5 x 4 x 3 x 2 x 1 = 120
As we know that all three vowels, i.e. OIA are different
Therefore, the number of ways by which the letters can be arranged is:
3! = 3 x 2 x 1 = 6
So, the required number of ways is:
120 x 6 = 720
So, the answer is Option A.
Question 3: Determine how many different ways can the letters of the word 'LEADING' be arranged so that the vowels always come together?
A. 420 B. 720
C. 920 D. 122
Solution: Here, we can find that there are 7 letters in the word 'LEADING'. The vowels present in it are 'E', 'A','I' in it and these 3 vowels should always come together. So, we can say that grouping can be done for these 3 vowels where it can be considered as a single letter, i.e. LDNG(EAI).
So, it can be assumed that the total letters as 5 where we can find that all these letters are different.
Therefore, the number of ways by which the letters can be arranged is
=5! = 5 × 4 × 3 × 2 × 1 = 120 = 5! = 5 × 4 × 3 × 2 × 1 = 120
We can see that all the vowels are different ie. E, A, I. Number of ways to arrange these vowels among themselves
=3! = 3 × 2 × 1 = 6 = 3! = 3 × 2 × 1 = 6
Therefore, the required number of ways
=120 × 6 = 720
So, the answer is Option B.
Question 4: There are ten patterns of chairs and eight patterns of tables of an event manager. Can you find out as to how many ways can he make a pair of table and chair?
A. 80 B. 110
C. 64 D. 100
Solution: According to the question, there are 8 patterns of tables and 10 patterns of chairs.
The number of ways a chair can be selected = 10 ways.
The number of ways a table can be selected = 8 ways.
So, we can select one chair and one table in 10 × 810 × 8 ways = 80 = 80 ways
So, the answer is Option A.
Question 5: Can you tell as to how many ways can three boys can be seated on five chairs?
A. 80 B. 30
C. 60 D. 120
Solution: There are three boys.
The number of ways the first boy can sit = 5
5
Now, we can find that there are 4 chairs remaining. The number of ways the second boy can sit = 4
5
4
So, as of now there are 3 chairs remaining. The number of ways the third boy can sit = 3
5
4
3
Therefore, the total number of ways in which 3 boys can be seated on 5 chairs
= 5 × 4 × 3 = 60
So, the answer is Option A.
Important Chapters:
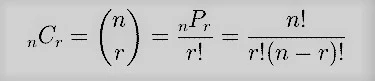
Permutation
Combination
It consists of the arrangement of numbers, people, digits, letters, colours, and alphabets,
It consists of the selection of food, clothes menu, subjects, team.
Picking of a pitcher, team captain and shortstop from a group.
Picking of three team members from a group.
Picking of two favourite colours, in order, from a colour brochure.
Picking of two colours from a colour brochure.
Picking the first, second and third place winners.
Picking the three winners.
= 6C4 + 6C3 × 4C1 + 6C2 × 4C2 + 6C1 × 4C3
= 6C2 + 6C3 × 4C1 + 6C2 × 4C2 + 6C1 × 4C1[∵ nCr = nC(n-r)]
The number of ways a chair can be selected = 10 ways.
5
5
4
5
4
3
Similar Questions
Permutation & Combination
View SolutionPermutation & Combination
View SolutionSeries Combination
View SolutionParallel Combination
View SolutionCombination OF Capacitors || Series Combination || Parallel Combination || Examples on Combination
View SolutionCombination of Resistors|Series Combination|Parallel Combination
View SolutionSeries Combination|Parallel Combination
View SolutionSeries Combination Of Cell|Parallel Combination Of Cell|Mixed Combination Of Cell
View SolutionQuestions|Combination Of Springs|Series Combination|Parallel Combination|Questions
View SolutionExercise Questions|Combination Of Spring|Parallel Combination Of Spring|Series Combination Of Spring
View Solution

