Question

Area and Perimeter of rhombus

Explanation

Area and Perimeter of Rhombus

Rhombus is a 2-Dimensional quadrilateral shape with four equivalent sides and four interior angles that are not necessarily 90 degrees. The sum of lengths of all the four sides of a rhombus is the perimeter of a rhombus. A square is also a type of rhombus because it fulfils all the condition that a rhombus possesses.

In a rhombus:

•           All four sides are of the same length

•           Opposite sides are parallel.

•           The height is a distance at right angles to two opposite sides.

•           Diagonals bisect each other at 90 degrees.

Area of a Rhombus

The area of a rhombus can be characterized as the measure of space enclosed by a rhombus on a flat surface or in a two-dimensional space. A rhombus is a quadrilateral with four equal sides where two pair of opposite sides are parallel. It is also known as symmetrical quadrilateral because all its four sides are equivalent.

How to find the Area of Rhombus?

There are different methods to calculate the area of a rhombus. There are three different formulae for rhombus area:

• Using Base and Height


• Using Diagonals


• Using Trigonometry

Area of Rhombus Formula

There are various formulas to find the area of a rhombus :

Different Formulas to Find Area of Rhombus
Base and Height	A = s × h
Diagonals	A = ½ × d1 × d2
Trigonometry	A = b2 × Sin(x)

Where,

• s à  length of any side


• h à height of rhombus


• d₁ à length of diagonal 1


• d₂ à length of diagonal 2


• x à any interior angle of the rhombus

Area of Rhombus with Base (any side of rhombus) and height

First, we will find the base (side of a rhombus) and the perpendicular height of the rhombus. Then we will multiply the base and height.

Example 1: Find the area of a rhombus if its base is 9 cm and height is 6 cm.

Solution:

Given,

Base, b = 9 cm

Height, h = 6 cm

Area, A = b × h

= 9 × 6 cm²

Area of rhombus= 54 cm²

Area of Rhombus with Diagonals

Suppose a rhombus PQRS, having two diagonals, i.e. d1= PR &  d2=QS.

First we will find the length of d1. It is the distance between P and R. The diagonals of a rhombus intersect each other at right angles making 4 right triangles at the centre of the rhombus. Second, we will find the length of d2, which is the distance between Q and S. Then multiply both the diagonals, d1 and d2. Finally, divide the result by 2.

Example 2: Find the area of a rhombus whose diagonals are 10 cm and 12 cm long.

Solution:

Given ,

Diagonal 1, d₁ = 10 cm

Diagonal 2, d₂ = 12 cm

Area of a rhombus = (d₁ × d₂) / 2

= (10 × 12) / 2

= 120 / 2

= 60 cm²

Thus, Area of a rhombus is 60 cm².

Area of Rhombus Using Trigonometry

In this case, first, we have to square the length of any of the sides, and then multiply it by Sine of any interior angles.

Example 3 Determine the area of a rhombus if the length of its side is 4 cm and one of its angle A is 30 degrees.

Solution:

Given,

Side, a = 4 cm

Angle A = 30 degrees

square of side a = 4 × 4= 16 cm²

Area, A= s² × sin (30)

A= 16 × 1/2

Area of rhombus = 8 cm²

Formula for Perimeter of a Rhombus

Perimeter of any geometrical shape is the total distance covered around the boundary, which can be determined by the algebraic sum of the length of each side. In a rhombus, all four sides have equivalent length; therefore, the perimeter becomes four times the length of a side.

Perimeter of Rhombus = 4 x Side

Related Videos:

• Area and Perimeter of rectangle


• Area and Perimeter of square


• Area and Perimeter of Trapezium


• Area and Perimeter of parallelogram


• Area and Perimeter of triangle


• Area and Perimeter of circle

Solved Problems on Rhombus Area and Perimeter Formula

Question 1: Find the perimeter of a rhombus having side as 6 cm ? 

Solution:

Given,

a = 6 cm

Perimeter of a rhombus = 4 × a

Perimeter of a rhombus = 4 × 6

Perimeter of a rhombus = 24 cm

Question 2: Find the area of the rhombus having each side equal to 10 cm and one of its diagonals equal to 12 cm.

Solution:

ABCD is a rhombus in which AB = BC = CD = DA = 10 cm

Diagonal AC = 12 cm (with O being the  intersection median point of the diagonal)

Therefore, AO = 6 cm

In ∆ AOD,

AD² = AO² + OD²

⇒ 10² = 6² + OD²

⇒ 100 -36 = OD²

⇒ 64 = OD²

⇒ OD = 8

Therefore, BD = 2 × OD

= 2 × 8

= 16 cm

Now, area of rhombus

= ½ × d₁ × d₂

= ½ × 12 × 16

Area of rhombus = 96 cm²

Question 3: The lengths of the diagonals of a rhombus are 20 and 48 meters. Find the perimeter of the rhombus.

Solution: Applying  the Pythagorean theorem to triangle BOC



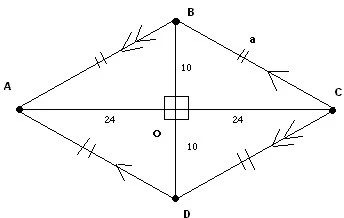
BC 2 = 10 2 + 24 2

BC2 = 100 + 576 m

BC2 = 676 = 26 m

Perimeter of Rhombus = 4 x side

= 4 x 26 m = 104 m

Question 4: Find the length of the diagonal of a rhombus if its area is 100 cm² and length of one diagonal is 20 cm.

Solution: 

Given: Area of rhombus = 100 cm² and Lets say d₁ = 20 cm.

Area of the rhombus,  A = (d₁ x d₂)/2,

100 = (20 x d₂)/2

100 = 10 x d₂

or  10 =  d₂

Important Chapters:

• NCERT Solutions for Maths


• NCERT Solution for Class 6 Maths Chapter Mensuration


• NCERT Solution for Class 8 Maths Chapter Mensuration