Line L1 is parallel to the line L2. Slope of L1 is 9. Also L3, is parallel to L4. Slope of L4 is 1−25 All these lines touch the ellipsex225+y29=1. Find the area of the parllelogram formed by these lines.
Step by step video & image solution for Line L_1 is parallel to the line L_2. Slope of L_1 is 9. Also L_3, is parallel to L_4. Slope of L_4 is 1/-25 All these lines touch the ellipsex^2/25+y^2/9=1. Find the area of the parllelogram formed by these lines. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Find the slope of line l which is parallel to X -axis . Also , find the slope of line n which is parallel to Y-axis .
View SolutionLet L be the set of all lines in XY -plane and R be the relation in L defined as R={(L1,L2):L1 is parallel to L2} . Show that R is an equivalence relation. Find the set of all lines related to the line y=2x+4 .
View Solution
Knowledge Check
The area of triangle formed by the lines l1andl2 and the x-axis is:
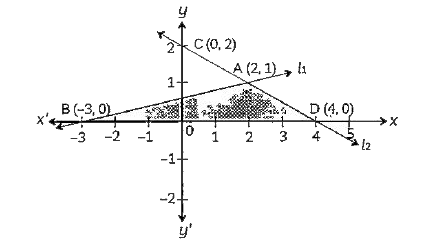 A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. unitsA line L passeds through the points (1,1)and(2,0) and another line L' passes through (12,0) and perpendicular to L. Then the area of the triangle formed by the lines L, L' and Y-axis is
A158B254C258D2516
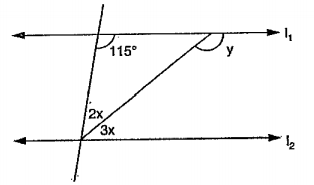
If line l1 is parallel to line l2 in the given figure , what is the value of y ?
View SolutionLet L be the set of all lines in XY=plane and R be the relation in L defined as R={(L1,L2):L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y=2x+4.
View SolutionLet L be the set of all lines in XY=plane and R be the relation in L defined as R={(L1,L2):L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y=2x+4.
View SolutionGiven equation of line L1 is y=4
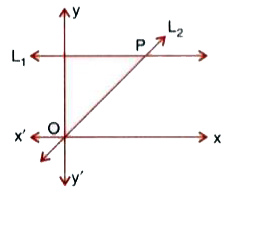
Write the slope of line L1 if L2 is the bisector of angle O.
View SolutionLet R be a relation on the set of all lines in a plane defined by (l1, l2)∈R <=> line l1 is parallel to line l2 . Show that R is an equivalence relation.
View SolutionLet R be a relation on the set of all line in a plane defined by (l1,l2)∈R⇔l1 is parallel to line l2. Show that R is an equivalence relation.
View Solution
