L लम्बाई तथा M द्रव्यमान का एक सर्वत्रसम पतला दण्ड चिकने क्षैतिज तल पर y-अक्ष के अनुदिश ऊर्ध्वाधर खड़ा है। दण्ड का निचला सिरा मूलबिन्दु (0, 0) पर है। समय t= 0 पर दण्ड में अल्प विक्षोभ उत्पन्न करने पर उसका निचला सिरा घन x- अक्ष की दिशा में चिकनी सतह पर फिसलने लगता है। तथा दण्ड गिरना प्रारम्भ हो जाता है।
(a) गिरने के दौरान दण्ड के द्रव्यमान केन्द्र का पथ क्या होगा?
(b) दण्ड पर निचले सिरे से दूरी पर स्थित एक बिन्दु के प्रक्षेप्य पथ का समीकरण ज्ञात कीजिए। इस बिन्दु के पथ का आकार क्या है?
The correct Answer is:(a) सरल रेखा (b) x2(L2−r)2+y2r2=1 दीर्घवृत
(a) दण्ड पर केवल दो बल कार्य कर रहे हैं, उसका भार Mg (ऊर्ध्वाधर नीचे की ओर) तथा स्पर्श बिन्दु B पर अभिलम्ब प्रतिक्रिया न (ऊर्ध्वाधर ऊपर की ओर)। दण्ड पर कोई क्षैतिज बल कार्य नहीं कर रहा है (अत: CM ऋणात्मक)
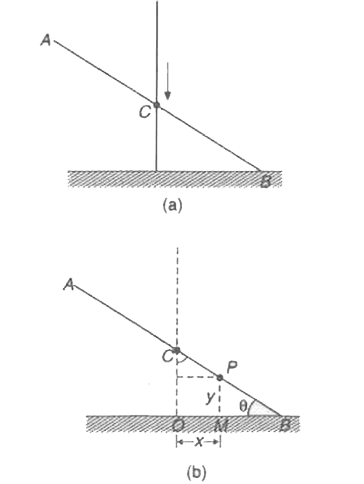
अंत: CM y-अक्ष की दिशा में ऊर्ध्वाधर निचे की और जायेगा अर्थार्त CM का मार्ग एक सरल रेखा है
(b) चित्र (b) से r दुरी पर स्थित बिंदु P(x,y) का पथ ज्ञात करना है
CB=L2
∴OB=(L2)cosθ
MB=rcosθ
x=OB−MB=cosθ(L2−r)
या cosθ=xL2−r.....(i)
इसी प्रकार y=rsinθ
या sinθ=yr......(ii)
समी (i) व् (ii) को वर्ग करके जोड़ने पर
sin2θ+cos2θ=x2(L2−r)2+y2r2
x2(L2−r)2+y2r2=1....(iii)
समी (iii) दीर्घवृत का समीकरण है। अंत: बिंदु P का पथ दीर्घवृताकार (Elliptical) होगा।
Topper's Solved these Questions
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - एकल पूर्णांक उत्तर प्रकार
2 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद III )
2 Videos
- धारा वैघुतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - धारा वैघुतिकी EXERCISE - क्षृंखलाबद्ध-बोधन प्रकार (अनुछेद I )
2 Videos
Similar Questions
हर प्रकार की गतिकीय समस्याओं के निश्लेषण के लिए कला-समष्टि चित्रा (Phase space diagrams) का उपयोग किया जाता है। प्रारम्भिक दशा, स्थिति व संवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझने में बहुत उपयोगी है। यहाँ हम एकविमीय सरल गतिकीय निकायों की बात करते हैं। इनके लिए कला-समष्टि समतल है जिसमें स्थिति X-अक्ष पर तथा संबेग Y-अक्ष पर रखते हैं, तब कुला-समष्टि चित्र इस समतल में एक x(t)-p(t) वक्र होगा। वक्र पर तीर समय बढ़ने की दिशा को दर्शाता है।
उदाहरण के लिए, स्थिर वेग से चल रहे कण के लिए कला- समष्टि चित्रा है, सरल रेखा है, जिसे चित्र में दिखाया गया है। चिह्न परिपाटी में स्थिति या संवेग को ऊपर (या दाहिने) ओर धनात्मक तथा नीचे (या बाई) ओर ऋणात्मक माना जाता है।
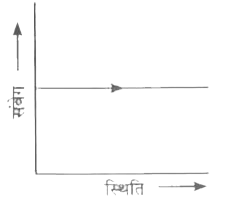
1. जमीन से ऊपर की ओर फेंकी गई गेंद का कला-समष्टि चित्रा है।
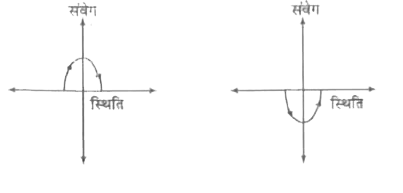
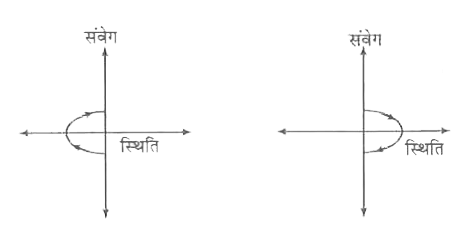
View Solutionएकसमान मोटाई की एक वृत्ताकार प्लेट का व्यास 56 सेमी है। प्लेट के एक सिरे से 42 सेमी व्यास का एक वृत्तीय भाग काटकर अलग कर दिया जाता है। शेष बचे भाग के द्रव्यमान केन्द्र की स्थिति ज्ञात कोजिए।
View Solutionअधिकतर पदार्थो का अपवर्तनांक, n>1 होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, sinθ1sinθ2=n2n1के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में εr व μr दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।
View Solutionh ऊँचाई वाले निर्वातित एक बेलनाकार कक्ष के दोनों छोरो पर दो दृढ़ चालक पट्टिकाएं है और उसका वक्रपृष्ठ अचालक है, जैसा की चित्र में दर्शाया गया है। कम भार वाली मुलायम पदार्थ से बनी हुई कई गोलाकार गोलियाँ, जिनकी सतह पर एक चालक पदार्थ की परत चढ़ी है, नीचे वाली पट्टिका पर रखी हुई है। इन गोलियों की त्रिज्या r<<h है। अब एक उच्च वोल्टता का स्त्रोत इस प्रकार से जोड़ा जाता है कि नीचे वाली पट्टिका पर +V0 एवं ऊपर वाली पट्टिका पर −V0 का विभव आ जाता है। चालक परत के कारण गोलियाँ आवेशित होकर पट्टिका के साथ समविभव हो जाती है जिसके कारण वे पट्टिका से प्रतिकर्षित होती है। अंततोगत्वा गोलियाँ ऊपरी पट्टिका से टकराती है, जहाँ पर गोलियों के पदार्थ की मुलायम प्रकृति के कारण प्रत्यवस्थान गुणांक को शून्य लिया जा सकता है। कक्ष में विद्युत क्षेत्र को समानान्तर पट्टिका वाले संधारित्र के माना जा सकता है। गोलियों की एक दूसरे से पारस्परिक क्रिया एवं टकराव को नगण्य माना जा सकता है (गुरुत्वाकर्षण नगण्य है।)

निम्नलिखित में से कौनसा कथन सत्य है?
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solution30 सेमी लम्बी एक छड़ AB दो लम्ब अक्षो पर इस प्रकार फिसलती है की छड़ का एक सिरा एक अक्ष पर एक दूसरा सिरा दूसरे अक्ष पर रहता है । छड़ के बिंदु C का बिन्दुपथ ज्ञात कीजिए जिससे AC तथा BC का अनुपात 2:1 रहे ।
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionपरवलय x2=8y पर एक स्पर्श रेखा,जो X-अक्ष की धनात्मक दिशा के साथ कोण θ बनती है, का सभीकरण है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solution
