In a school, 80 students like Maths, 90 students like Science, 82 students like History, 21 like both Maths and Science, 19 like both Science and History 20 like both Maths and History and 8 liked all the three subjects. If each student like atleast one subject, then find (i) the number of students in the school (ii) the number of students who like only one subject.Solution in Tamil
Step by step video & image solution for In a school, 80 students like Maths, 90 students like Science, 82 students like History, 21 like both Maths and Science, 19 like both Science and History 20 like both Maths and History and 8 liked all the three subjects. If each student like atleast one subject, then find (i) the number of students in the school (ii) the number of students who like only one subject. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SET LANGUAGEBOOK - SURA PUBLICATIONCHAPTER - SET LANGUAGEEXERCISE - EXERCISE 1.7
26 Videos
- SET LANGUAGEBOOK - SURA PUBLICATIONCHAPTER - SET LANGUAGEEXERCISE - TEXT BOOK ACTIVITIES
2 Videos
- SET LANGUAGEBOOK - SURA PUBLICATIONCHAPTER - SET LANGUAGEEXERCISE - EXERCISE 1.5
19 Videos
- REAL NUMBERS BOOK - SURA PUBLICATIONCHAPTER - REAL NUMBERS EXERCISE - UNIT TEST
19 Videos
- STATISTICSBOOK - SURA PUBLICATIONCHAPTER - STATISTICSEXERCISE - Section -C
2 Videos
Similar Questions
Which of the following is correct?
View SolutionDiscuss and give as many examples of collections from your daily life situations, which are sets and which are not sets.
View SolutionUsing the adjacent venn diagram, find the following sets :
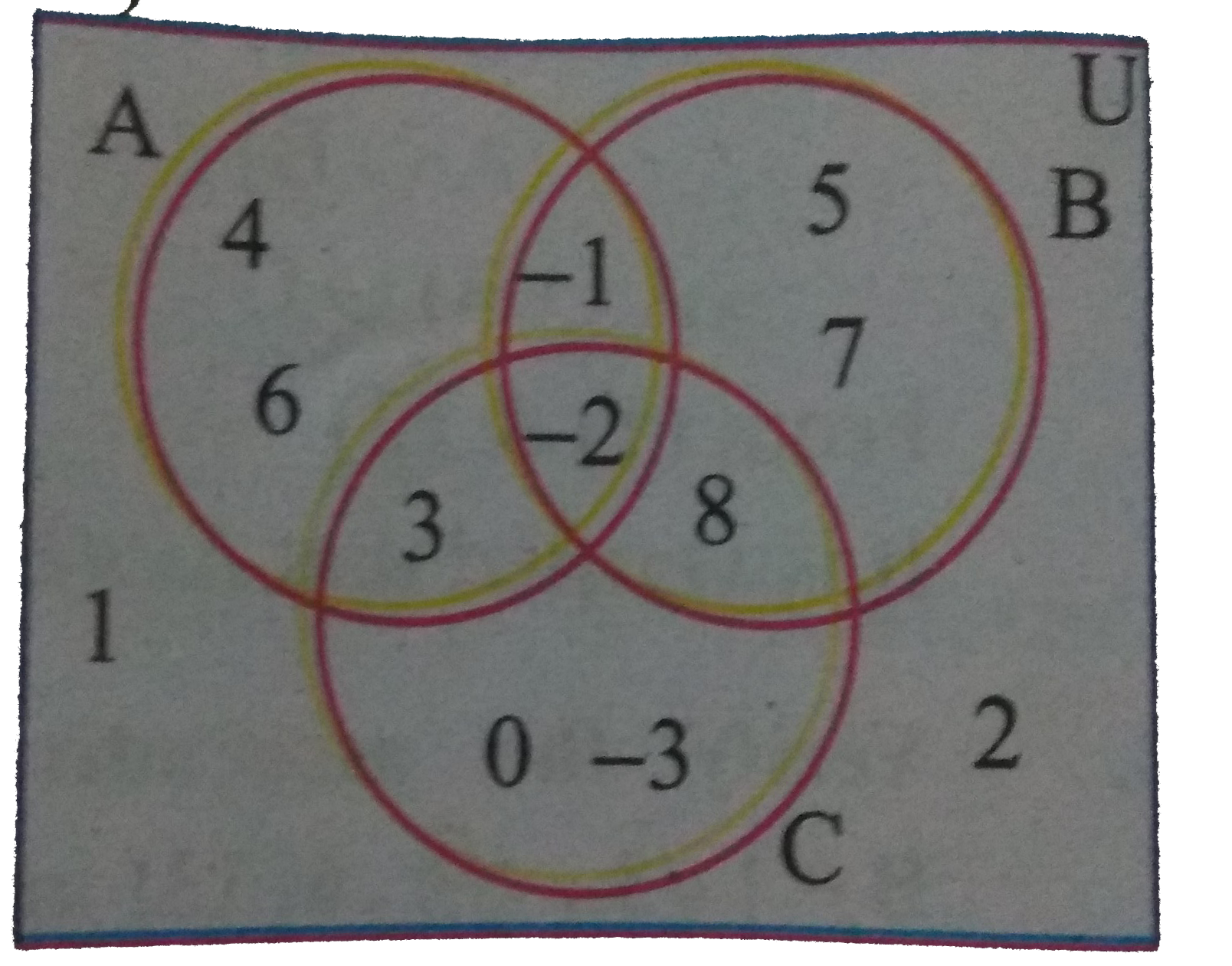
(i) A - B
(ii) B - C
(iii) A'∪B'
(iv) A'∩B'
(v) (B∪C)'
(vi) A−(B∪C)
(vii) A−(B∩C)
View SolutionWhich one of the following , regarding sum of two irrational number , is true ?
View SolutionCalculate the mean of the following distribution using Assumed Mean Method.

View SolutionIn a class of 120 students.If 40 of them like Science' and 80 of them like 'Mathematics', then the number of students who like both Mathematicsand,' and Science' must be _(-)
View SolutionIn a class of 35 students, 18 students opt Maths, 12 students opt Maths but not Science. Find the number of students who opt both subjects. Also find the number of students two opt Science but not Maths. It is given that each student opt atleast one subject.
View SolutionIn a class , 40 student like Maths, 50 students like Physics and 60 students like Chemistry. 30 students like both Maths and Physics, 20 students like both Physics and Chemistry and none of them like both Maths of Chemistry . Find the total number of students who like only Maths, only Physics and only Chemistry.
View SolutionIn a class of 60 students, 30 students like Mathematics, 25 like Science and 15 like both. Then, the number of students who like either Mathematics or Science is
View SolutionIn a class of 50 students 32 likes Mathematics , 24 like Science and 12 like both . Find the number of students who like neither of the two subjects.
View SolutionOut of 100 students, 40 does not like maths and 60 like maths. What is the chance of choosing a student randomly that he/she likes maths?
View Solution35 জন ছাত্রের একটি শ্রেণির তথ্যানুসন্ধানে দেখা গেলো যে, 17 জন ছাত্র গণিত পছন্দ করে এবং 10 জন ছাত্র গণিত পছন্দ করে কিন্ত জীববিদ্যা পছন্দ করেনা|কতজন ছাত্র জীববিদ্যা পছন্দ করে তা নির্ণয় করো, দেওয়া আছে যে, শ্রেণির প্রত্যেক ছাত্র কমপক্ষে একটি বিষয় পছন্দ করে|
View Solution35 জন ছাত্রের একটি শ্রেণির তথ্যানুসন্ধানে দেখা গেলো যে, 17 জন ছাত্র গণিত পছন্দ করে এবং 10 জন ছাত্র গণিত পছন্দ করে কিন্ত জীববিদ্যা পছন্দ করেনা|কতজন ছাত্র জীববিদ্যা পছন্দ করে কিন্ত গণিত পছন্দ করে না, তা নির্ণয় করো, দেওয়া আছে যে, শ্রেণির প্রত্যেক ছাত্র কমপক্ষে একটি বিষয় পছন্দ করে|
View SolutionIn a school 80 students like chocolate, 40 like coffee if the number of students doesn't like any of them is equal to the number of students who like both of them then what is the total number of students in the school?
View SolutionIn a class of 30 students, 12 students like emboidary, 16 students like physics and 18 student like history. If all students select at least one subject and none of them select all the subject then find the number of students select 2 subject.
View Solution
