The potential energy of a particle varies with distance x from a fixed origin as V=A√XX+B where A and B are constants . The dimension of AB are
[ML5/2T−2],[L]
[MLT−2],[L2]
[L],[ML3/2T−2]
[L2],[MLT−2]
The correct Answer is:A
Step by step video, text & image solution for The potential energy of a particle varies with distance x from a fixed origin as V= (Asqrt(X))/(X + B) where A and B are constants . The dimension of AB are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - B)31videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - C)31videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE20videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)10videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTECHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))1videos
WAVE OPTICS
Similar Questions
The potential energy 'U' of a particle veries with distance 'x' from a fixed origin as U=AXx2+B. Where A and B are dimensional constants. Find the dimension of length in AB.
View SolutionThe potential energy of a particle varies with distance 'x' as U=(Ax^(1/2))/(x^(2)+B),where A and B are constants.The dimensional formula for A times B is [M^(a)L^(b)T^(c)] then a=
View Solution
Knowledge Check
- Question 1 - Select One
The potential energy U of a particle varies with distance x from a fixed origin as U=A√xx2+B where A and B are dimensional constants. The dimensional formula for AB is
A[M1L7/2T−2]B[M1L11/2T−2]C[M1L5/2T−2]DM1L9/2T−2] - Question 2 - Select One
The potential energy of a particle varies with distance x from a fixed origin as U=A√xx2+B, where AandB are dimensional constants , then find the dimensional formula for AB.
A[ML11/2T−1]B[ML11T−2]C[ML7/2T−2]D[ML11/2T−2] - Question 3 - Select One
The potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle isAB/ABB/2AC2A/BDA/B
The potential energy of a particle depends on its x-coordinates as U=A√xx2+B, where A and B are dimensional constants. What will be the dimensional formula for A/B?
View SolutionThe potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by V(r)=kr2/2, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
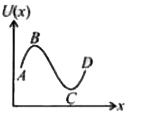 View Solution
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
 View Solution
View SolutionThe potential energy of a particle in a force field is
U=Ar2−Br
where A and B are positive constants and r is the distance of particle from the centre of the field. For stable equilibirum, the stable equilibrium , the distance of the particle isView Solution

