Question

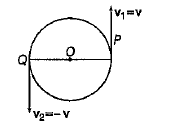
A particle of mass m moves with constant speed v on a circular path of radius r. Find magnitude of average force on it in half revolution.

Explanation

To find the magnitude of the average force on a particle of mass $$m$$ moving with constant speed $$v$$ on a circular path of radius $$r$$ during half a revolution, we can follow these steps:

Step 1: Understand the motion
The particle moves in a circular path with constant speed \( v \). During half a revolution, the particle will move from one point on the circle to the opposite point.

Step 2: Determine the change in velocity
The initial velocity vector \( \vec{v_i} \) can be represented as:
- At the starting point (let's say at the top of the circle): \( \vec{v_i} = v \hat{j} \)

After half a revolution, the particle reaches the bottom of the circle, where its velocity vector \( \vec{v_f} \) is:
- At the bottom point: \( \vec{v_f} = -v \hat{j} \)

Step 3: Calculate the change in velocity
The change in velocity \( \Delta \vec{v} \) is given by:
\( \Delta \vec{v} = \vec{v_f} - \vec{v_i} = (-v \hat{j}) - (v \hat{j}) = -2v \hat{j} \)

Step 4: Determine the time taken for half revolution
The time \( t \) for one complete revolution is given by:
\( t = \frac{2\pi r}{v} \)
Thus, the time for half a revolution is:
\( t_{\text{half}} = \frac{t}{2} = \frac{\pi r}{v} \)

Step 5: Calculate the average acceleration
The average acceleration \( \vec{a}_{\text{avg}} \) is defined as the change in velocity divided by the time taken:
\( \vec{a}_{\text{avg}} = \frac{\Delta \vec{v}}{t_{\text{half}}} = \frac{-2v \hat{j}}{\frac{\pi r}{v}} = \frac{-2v^2}{\pi r} \hat{j} \)

Step 6: Calculate the average force
Using Newton's second law, the average force \( \vec{F}_{\text{avg}} \) can be calculated as:
\( \vec{F}_{\text{avg}} = m \vec{a}_{\text{avg}} = m \left( \frac{-2v^2}{\pi r} \hat{j} \right) = \frac{-2mv^2}{\pi r} \hat{j} \)
The magnitude of the average force is:
\( F_{\text{avg}} = \left| \vec{F}_{\text{avg}} \right| = \frac{2mv^2}{\pi r} \)

Final Answer
The magnitude of the average force on the particle during half a revolution is:
\( F_{\text{avg}} = \frac{2mv^2}{\pi r} \)