A : It makes easier to walk on slippery muddy road if we throw some sand on it.
R : On throwing sand, frictional force of the surface increases.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion
If Assertion is true statement but Reason is false
If both Assertion and Reason are false statements
Step-by-Step Solution:
1. Understanding the Problem: The question states that it is easier to walk on a slippery muddy road if sand is thrown on it. We need to analyze both the assertion (A) and the reason (R) provided.
2. Analyzing the Assertion (A): The assertion claims that throwing sand on a slippery muddy road makes it easier to walk. This is true because a muddy road is typically slippery due to a low coefficient of friction (μ). When μ is low, the frictional force is also low, making it difficult to walk.
3. Analyzing the Reason (R): The reason states that throwing sand increases the frictional force of the surface. This is also true. When sand is added to the muddy surface, it increases the coefficient of friction (μ) between the shoes and the ground, which in turn increases the frictional force.
4. Connecting A and R: The assertion (A) is correct because it describes the situation accurately, and the reason (R) is also correct as it explains why the assertion is true. The increase in frictional force due to the addition of sand makes walking easier on the muddy road.
5. Conclusion: Both the assertion and the reason are correct, and the reason correctly explains the assertion. Therefore, the answer is that both A and R are true, and R is the correct explanation of A.
Final Answer:
Both the assertion (A) and the reason (R) are correct, and R is the correct explanation of A.
---
Both the assertion (A) and the reason (R) are correct, and R is the correct explanation of A.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Use your ideas about pressure to explain why it is easier to walk on soft sand if you have flat shoes tather than shoes with sharp heels.
View SolutionYou move a stone of glass on the cemented floor, marble floor, water, towel and on ice. The force of friction acting on the different surfaces in increasing orde3r will be:
View Solution
Knowledge Check
When liquid medicine of density ρ is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of te drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surfacetension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If the radius of the opening of the dropper is r, the vertical force due to the surface tension on the top of radius R (assuming r<<R) isA2πrTB2πrRTC2πr2TRD2πR2TrState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here r is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assuming coefficient of friction between sphere and the surface. Mass of sphere is m.
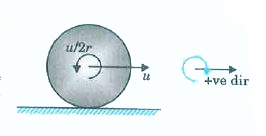
At what time sphere stops rotating for a moment?Au5μgB2u5μgC3u7μgD2u7μgState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
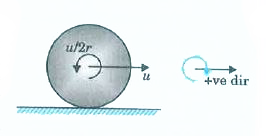
At what time sphere starts pure rolling?A2u7μgB3u5μgC3u7μgD5u7μg
A rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is μ. Let the mass of the box be m .
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to α>θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.

What will be the speed of sphere when it starts pure rolling?
View SolutionA : When a man is walking on a rough road, that work done by frictiona force is zero.
R : Frictional force acts in the direction of the motion of the man in this case.
View SolutionWhen liquid medicine ρ is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop froms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is osperical becaus ethat requires a minimum increase in its surface energy. To datermine the size., we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force become smaller than the wight of the drop, the drop gets detached from the droppr.
If the radius of the opening of the dropper is r, the verital force due to the surface tension on the drop of radius R (assuming r<<R) is :
View SolutionWhen liquid medicine of density ρ is to put in the eye, it is done with the help of a dropper. As the bulp on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If the radius of the opening of the dropper is r, the vertical force due to the surface tension on the drop of radius R (assuming r ltltR) is
View Solution
