A point object of mass m is kept at (a, 0) along x-axis. What mass should be kept at (-3a,0), so that centre of mass lies at origin ?
m
2m
m3
3m
The correct Answer is:C
To find the mass that should be placed at (-3a, 0) so that the center of mass of the system lies at the origin, we can follow these steps:
Step 1: Understand the System
We have two masses:
- Mass m located at (a,0)
- Mass M located at (−3a,0)
Step 2: Write the Formula for Center of Mass (CM)
The formula for the center of mass xcm of a system of particles along the x-axis is given by:
xcm=m1x1+m2x2m1+m2
Where:
- m1 and m2 are the masses,
- x1 and x2 are their respective positions.
Step 3: Set the Condition for Center of Mass at the Origin
We want the center of mass to be at the origin, so we set xcm=0:
0=m⋅a+M⋅(−3a)m+M
Step 4: Simplify the Equation
Now, multiply both sides by (m+M) to eliminate the denominator:
0=m⋅a−3M⋅a
Step 5: Factor Out Common Terms
Since a is not zero, we can factor it out:
0=a(m−3M)
Step 6: Solve for M
For the equation to hold true, we need:
m−3M=0
This leads to:
m=3M
Step 7: Rearranging the Equation
Now, we can express M in terms of m:
M=m3
Conclusion
Thus, the mass M that should be placed at (−3a,0) so that the center of mass lies at the origin is:
M=m3
---
We have two masses:
- Mass m located at (a,0)
- Mass M located at (−3a,0)
The formula for the center of mass xcm of a system of particles along the x-axis is given by:
- m1 and m2 are the masses,
- x1 and x2 are their respective positions.
We want the center of mass to be at the origin, so we set xcm=0:
Now, multiply both sides by (m+M) to eliminate the denominator:
Since a is not zero, we can factor it out:
For the equation to hold true, we need:
Now, we can express M in terms of m:
Thus, the mass M that should be placed at (−3a,0) so that the center of mass lies at the origin is:
Similar Questions
A point mass m is located at (0,a). Where should the 2m mass be kept, so that centre of mass lies at origin
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View Solution
Knowledge Check
- Question 1 - Select One or More
A point object is kept at (1,0,0). A circular plane mirror of radius 1m is kept in yz-plane such that its centre is at the origin. The reflecting side faces positive x-axis At which of the following points can the image of the object be seen?
A(-0.5,0,0.5)B(2,2,2)C(1,1.5,1.5)D(1,-1,1.5) - Question 2 - Select One or More
Two small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
Aif particle R is displaced along x-axis it will start oscillating.Boscillations of R along x-axis are simple harmonic in natureCif R is displaced of R along y-axis, it starts oscillatingDoscillations along y-axis may be simple harmonic in nature. - Question 3 - Select One
Two rods of equal lengths(l) and equal mass M are kept along x and y axis respectively such that their centre of mass lie at origin. The moment of inertia about an line y = x, is
Aml23Bml24Cml212Dml26
Consider an infinite distribution of point masses (each of mass m) placed on x-axis as shown in the diagram. What is the gravitational force acting on the point mass placed at the origin ?
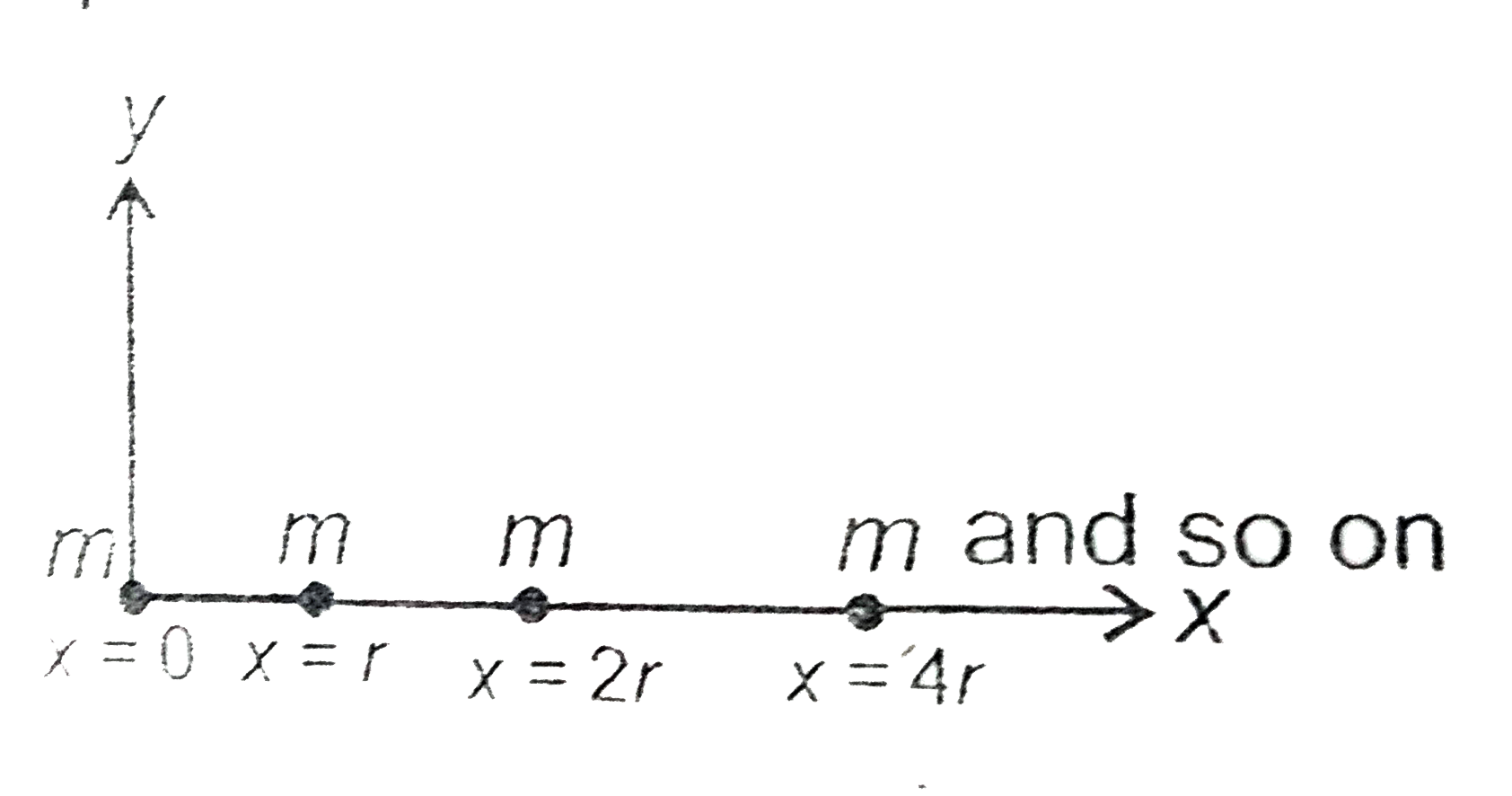 View Solution
View SolutionTwo bodies of masses 3 kg and 4 kg are moving along X axis. At a time t, the bodics are at a distance of 2 m and 3 m from the origin and has velocities of 2ms−1and−3ms−1. Calculate the position and velocity of centre of mass. What will be the total momentum of the system?
View SolutionFour point masses each mass m kept at the vertices of a square. A point mass m is kept at the point of intersection of the diagonal of a square. What be the force experienced by central mass m ?
View SolutionA large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
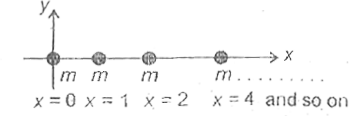 View Solution
View SolutionA system consisting of two masses connected by a massles rod, lies along the X axis. A body of mass 0.4 kg is kept at a distnce x=2m and another body of mass 0.6 kg is kept at the distance x=6 m from the origin. What is the x-coordinate of the centre of mass?
View Solution

