A force F doubles the length of wire of cross-section a The Young modulus of wire is
Fa
F3a
F2a
F4a
To find the Young's modulus of a wire that doubles in length when a force F is applied, we can follow these steps:
Step 1: Define the initial conditions
Let:
- Initial length of the wire = L
- Cross-sectional area of the wire = A
- Force applied = F
Step 2: Determine the final length of the wire
When the force F is applied, the length of the wire doubles. Thus:
- Final length = 2L
Step 3: Calculate the change in length
The change in length ΔL can be calculated as:
ΔL=Final length−Initial length=2L−L=L
Step 4: Calculate the stress
Stress (σ) is defined as the force applied per unit area. Therefore:
σ=FA
Step 5: Calculate the strain
Strain (ϵ) is defined as the change in length divided by the original length. Thus:
ϵ=ΔLL=LL=1
Step 6: Calculate Young's modulus
Young's modulus (Y) is defined as the ratio of stress to strain:
Y=StressStrain=σϵ
Substituting the values we calculated:
Y=FA1=FA
Final Answer
The Young's modulus of the wire is:
Y=FA
---
Let:
- Initial length of the wire = L
- Cross-sectional area of the wire = A
- Force applied = F
When the force F is applied, the length of the wire doubles. Thus:
- Final length = 2L
The change in length ΔL can be calculated as:
ΔL=Final length−Initial length=2L−L=L
Stress (σ) is defined as the force applied per unit area. Therefore:
σ=FA
Strain (ϵ) is defined as the change in length divided by the original length. Thus:
ϵ=ΔLL=LL=1
Young's modulus (Y) is defined as the ratio of stress to strain:
Y=StressStrain=σϵ
Substituting the values we calculated:
Y=FA1=FA
The Young's modulus of the wire is:
Y=FA
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-A)
52 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-B)
24 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - J)
1 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTECHAPTER - Mock test 03EXERCISE - EXAMPLE
37 Videos
Similar Questions
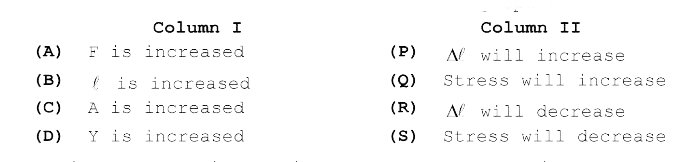
A wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
View SolutionAn object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
View Solution
Knowledge Check
In CGS system, the Young's modulusm of a steel wire is 2×1012. To double the length of a wire of unit cross-section area, the force
A4×106 dynesB2×1012 dynesC2×1012 newtonsD2×108 dynesSpeed of transverse wave on a straight wire (mass m, length l , area of cross-section A) is. If the young’s modulus of wire is Y, the extension of wire over its natural length, is independent of
AlBmCADYTwo wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
A1B2C12D√2
A stone of mass m is attached to one end of a wire of cross-sectional area A and Young's modulus Y. The stone is revolved in a horizontal circle at a speed such that the wire makes an angle θ with the vertical. The strain produced in the wire will be
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionIf the length of a wire is doubled, then its Young's modulus
View SolutionA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View Solution
