The raise in the temperature of a given mass of an ideal gas at constant pressure and at temperature 27∘ to double its volume is
327∘C
54∘C
300∘C
600∘C
The correct Answer is:C
To solve the problem of finding the rise in temperature of a given mass of an ideal gas at constant pressure when its volume is doubled, we can follow these steps:
Step 1: Understand the relationship between volume and temperature
For an ideal gas at constant pressure, the volume (V) is directly proportional to the absolute temperature (T) according to Charles's Law. This can be expressed as:
V1T1=V2T2
where V1 and T1 are the initial volume and temperature, and V2 and T2 are the final volume and temperature.
Step 2: Convert the initial temperature to Kelvin
The initial temperature given is 27∘C. To convert this to Kelvin, we add 273:
T1=27+273=300K
Step 3: Define the initial and final volumes
Let the initial volume be V1=V and the final volume be V2=2V (since the volume is doubled).
Step 4: Set up the equation using Charles's Law
Using the relationship from Step 1:
VT1=2VT2
Step 5: Simplify the equation
We can cancel V from both sides (assuming V≠0):
1T1=2T2
Step 6: Rearrange to find T2
Rearranging gives:
T2=2T1
Step 7: Substitute the value of T1
Substituting T1=300K:
T2=2×300=600K
Step 8: Convert the final temperature back to Celsius
To convert T2 back to Celsius:
T2=600−273=327∘C
Step 9: Calculate the rise in temperature
The rise in temperature ΔT is given by:
ΔT=T2−T1
Substituting the values:
ΔT=327−27=300∘C
Final Answer
The rise in temperature is 300∘C.
---
For an ideal gas at constant pressure, the volume (V) is directly proportional to the absolute temperature (T) according to Charles's Law. This can be expressed as:
V1T1=V2T2
where V1 and T1 are the initial volume and temperature, and V2 and T2 are the final volume and temperature.
The initial temperature given is 27∘C. To convert this to Kelvin, we add 273:
T1=27+273=300K
Let the initial volume be V1=V and the final volume be V2=2V (since the volume is doubled).
Using the relationship from Step 1:
VT1=2VT2
We can cancel V from both sides (assuming V≠0):
1T1=2T2
Rearranging gives:
T2=2T1
Substituting T1=300K:
T2=2×300=600K
To convert T2 back to Celsius:
T2=600−273=327∘C
The rise in temperature ΔT is given by:
ΔT=T2−T1
Substituting the values:
ΔT=327−27=300∘C
The rise in temperature is 300∘C.
Topper's Solved these Questions
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - B Objective Type Questions
30 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - C Previous Years Questions
21 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE
10 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
Knowledge Check
For given mass of an ideal gas at constant temperature
AP vs V graph is a straight line passing through originBP vs 1V graph is a rectangular hyperbolaCPV vs P graph is a straight line passing through originDPV vs V graph is a straight lineAt constant temperature, in a given mass of an ideal gas -
AThe ratio of pressure and volume always remains constantBVolume always remains constantCpressure always remains constantDThe product of pressure and volume always rmains constantAt constant temperature, in a given mass of an ideal gas -
AThe ratio of pressure and volume always remains constantBVolume always remains constantCPressure always remains constantDThe product of pressure and volume always remains constant
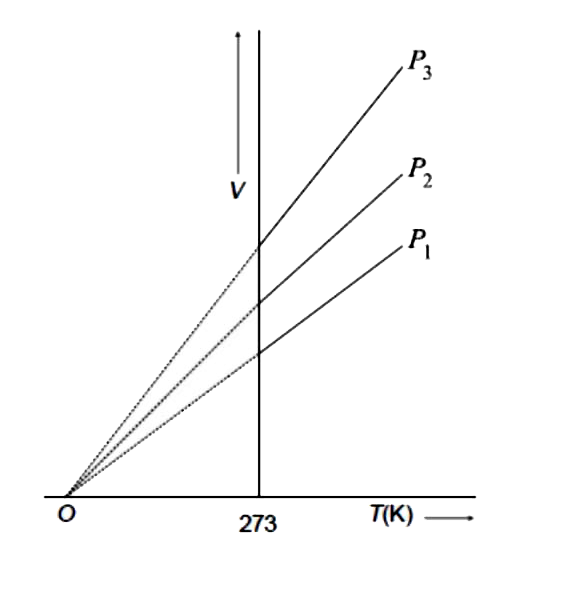
The volume-temperature graphs of a given mass of an ideal gas at constant pressure are shown below. What is the correct order of pressure ?

View SolutionThe volume-temperature graphs of a given mass of an ideal gas at constant pressures are shown below. What is the correct order of pressures ?
View SolutionIf both the temperature and the volume of an ideal gas are doubled, the pressure
View SolutionAt what temperature would the volume of a given mass of a gas at constant pressure will be twice of its volume at 0∘C
View SolutionIf the pressure of a given mass of gas is reduced to half and temperature is doubled simultaneously the volume will be
View Solution
