भुजा a वाले एक समबाहु त्रिभुज के शीर्ष A और B पर समान आवेश q है। त्रिभुज के बिन्दु C पर विद्युत क्षेत्र का परिमाण ज्ञात कीजिये।
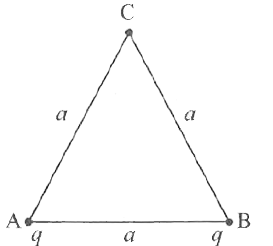
माना कि बिन्दु A पर स्थित आवेश q तथा बिन्दु B पर स्थित आवेश q के कारण बिन्दु P पर विद्युत क्षेत्र की तीव्रता क्रमशः →EA तथा →EB है। तब
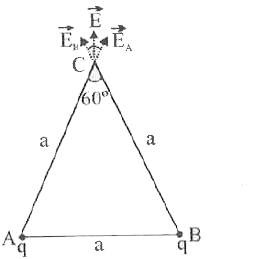
EA=EB=Kqa2
∴ बिन्दु C पर परिणामी विद्युत क्षेत्र का परिमाण
E=√E2A+E2B+2EAEBcos60∘
∵EA=EB
∴E=√E2A+E2A+2EAEA(1/2)
=√3E2A=√3EA
∴E=√3Kqa2=14π∈0√3qa2
Topper's Solved these Questions
- विद्युत क्षेत्र BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत क्षेत्र EXERCISE - अन्य महत्वपूर्ण प्रश्न (वस्तुनिष्ठ प्रश्न )
6 Videos
- विद्युत क्षेत्र BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत क्षेत्र EXERCISE - अन्य महत्वपूर्ण प्रश्न (लघूत्तरात्मक प्रश्न )
7 Videos
- विद्युत क्षेत्र BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत क्षेत्र EXERCISE - पाठ्यपुस्तक के प्रश्न- उत्तर (निबंधात्मक प्रश्न )
5 Videos
- विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी EXERCISE - अन्य महत्वपूर्ण प्रश्न ( आंकिक प्रश्न )
5 Videos
- विद्युत चुम्बकीय प्रेरणBOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत चुम्बकीय प्रेरणEXERCISE - अन्य महत्वपूर्ण प्रश्न ( आंकिक प्रश्न )
11 Videos
Similar Questions
किसी प्रोटॉन पर उसके भार के बराबर विद्युत बल लगाने के लिए विद्युत क्षेत्र की तीव्रता का मान है -
View Solutionआवेशित काँच की छड़ कागज के टुकड़े को क्यों आकर्षित करती है ?
View Solutionदो आवेशों के मध्य स्थिर विद्युत बल के कूलॉम के नियम को परिभाषित कीजिये तथा इसकी सीमाये बताइये। इस नियम द्वारा इकाई आवेश की परिभाषा दीजिये।
View Solutionएक भू - केंद्र अभिग्राही (a ) 5 MHz तथा (b ) 100 MHz के संकेत ग्रहण कर रहा है जिन्हे 300 m ऊंचाई पर स्थित्त भू - प्रेषित्र से संप्रेषित किया जा रहा है दोनों के बीच 100 km दुरी है पता लगाइए की संकेत अंतरिक्ष तरंगो के रूप में व्योम तरंग से या उपग्रह ट्रांसपोंडर ( प्रेषानुकर ) से प्राप्त किए जा रहे है पृथ्वी की त्रिज्या ≈6.4×106m आयनमंडल का mmax =1012m3 ।
View Solutionभंवर धाराओं की उत्पति समझाये
View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionकिसी त्रिभुज के शीर्षो से समान दूरी पर स्तिथ बिंदु का नाम लिखि।
View Solutionसदिशों के प्रयोग द्वारा उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(2,3,5),B(3,5,8) और C(2,7,8) हैं |
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionकिसी त्रिभुज एब्स के शीर्ष A(−3,4),B(6,−2) और C(2,5) है। बिन्दु A से होकर जाने वाली माध्यिका का समीकरण ज्ञात कीजिए ।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
View Solutionयदि →a,→b तथा →c समबाहु त्रिभुज के शीर्ष के स्थिति सदिश हो जिसका लम्ब केंद्र मूलबिंदु है , तो →a+→b+→c का मान ज्ञात कीजिए।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solution
