एक समांतर प्लेट संधारित्र जिसकी वृताकार प्लटो की त्रिज्या 1m है धारिता 1nF है समय t =0 पर इसको आवेशित करने के लिए $R = 1 M Ω$ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोड़ा गया है ( चित्र ) $10^{- 3} S$ के पश्चात संधारित्र के बीच में दोनों प्लेटो के केंद्र एवं परिकलन कीजिए [क्षण t पर संधारित्र पर आवेश $q (t) = C V [1 - exp (- t / t)$ होता है जहाँ समय नियतांक $τ = C R$ है

Text Solution

Verified by Experts

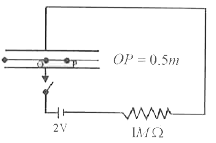
दिया है प्लेटो की त्रिज्या $r = 1$ मी , धारिता $C = n F = 1 \times 10^{- 9}$ फेर्ड प्रतिरोध $R = 1 M Ω, V = 2$ वोल्ट समय $t = 10^{- 3}$ सेकंड
अंत : CR परिपथ का काल नियतांक
$τ = C R = 1 \times 10^{- 9} \times 1 \times 10^{6} = 10^{- 3}$ सेकंड
प्लेट का क्षेत्रफल $A = π r^{2} = 3 .14$ मी $^{2}$ $= π (∵ r = 1$ मी )
$∵$ किसी क्षण t पर प्लेटो के मध्य विधुत क्षेत्र
$E = \frac{σ}{\in_{0}} = \frac{q}{A \in_{0}} = \frac{q}{π \in_{0}}$
अब यदि हम $1 / 2$ मी त्रिज्या के एक वृताकार लूप जो की बिंदु P से गुजरे तथा जिसका केंद्र बिंदु O पर हो की कल्पना करते है लूप के प्रत्येक बिंदु पर चुम्बकीय क्षेत्र एक समान होगा तथा इसकी दिशा लूप के तल के अनुदिश होगी।
लूप से गुजरने वाला फ्लक्स $Φ_{E} = E a$ (a लूप का क्षेत्रफल )
$Φ_{E} = \frac{q}{π \in_{0} (π \times {(\frac{1}{2})}^{2}) = \frac{q}{4 \in_{0}}}$
अंत : विस्थापन धारा $I_{d} = \in_{0} \frac{d ϕ_{E}}{d t} = \in_{0} \frac{d}{d t} (\frac{q}{4 \in_{0}}) = \frac{1}{4} \frac{d q}{d t}$
q का मान रखने पर
$I_{d} = \frac{d}{d t} [C V (1 - e^{- t / τ}] = \frac{C V}{4 τ} e^{- t / τ}$
या $I_{d} = \frac{1 \times 10^{- 9} \times 2}{4 \times 10^{- 3}} e^{- 1} = 0 .5 \times 10^{- 6}$ e ^(-1 ) $ऐ म ् प ि य र न ि य म स े < b r >$ Bxx 2 pi r_1 = mu _0 (I_c +I_d ) $ज ह ा$ r _1 = $ल ू प क ी त ् र ि ज ् य ा) < b r >$ B= (mu _0 ) / (2 pi r _1 ) (I _c +I_d ) $द ि य ा ह ै प ् ल े ट ो क ी त ् र ि ज ् य ा$ r =1 $म ी, ध ा र ि त ा$ C = nF = 1 xx 10 ^(-9 ) $फ े र ् ड प ् र त ि र ो ध$ R = 1M Omega ,V =2 $व ो ल ् ट स म य$ t =10 ^(-3 ) $स े क ं ड < b r > अ ं त : C R प र ि प थ क ा क ा ल न ि य त ा ं क < b r >$ tau = CR = 1 xx 10 ^(-9 )xx 1xx 10 ^6 = 10 ^(-3 ) $स े क ं ड < b r > प ् ल े ट क ा क ् ष े त ् र फ ल$ A = pi r ^2 = 3 .14 $म ी$ ""^2 =pi " " ( :' r =1 $म ी) < b r >$ :' $क ि स ी क ् ष ण t प र प ् ल े ट ो क े म ध ् य व ि ध ु त क ् ष े त ् र < b r >$ E = ( sigma )/(in _0 ) = (q )/(A in _0 ) = (q )/ (pi in _0 ) $< b r > अ ब य द ि ह म$ 1 //2 $म ी त ् र ि ज ् य ा क े ए क व ृ त ा क ा र ल ू प ज ो क ी ब ि ं द ु P स े ग ु ज र े त थ ा ज ि स क ा क े ं द ् र ब ि ं द ु O प र ह ो क ी क ल ् प न ा क र त े ह ै ल ू प क े प ् र त ् य े क ब ि ं द ु प र च ु म ् ब क ी य क ् ष े त ् र ए क स म ा न ह ो ग ा त थ ा इ स क ी द ि श ा ल ू प क े त ल क े अ न ु द ि श ह ो ग ी । < b r > ल ू प स े ग ु ज र न े व ा ल ा फ ् ल क ् स$ Phi _E =Ea $(a ल ू प क ा क ् ष े त ् र फ ल) < b r >$ Phi _E = (q )/(pi in _0 (pi xx ((1 )/(2 ))^2 )= (q )/(4 in _0 ) $< b r > अ ं त : व ि स ् थ ा प न ध ा र ा$ I _d = in _0 (d phi _E )/( dt ) =in _0 (d )/(dt )((q )/(4 in _0 ))=1 /4 (dq )/(dt ) $< b r > q क ा म ा न र ख न े प र < b r >$ I _d = (d )/ (dt ) [ CV (1 -e ^(-t // tau ) ] = (CV )/(4 tau ) e ^(-t // tau ) $< b r > य ा$ I _d = (1 xx 10 ^(-9 )xx 2 )/(4 xx 10 ^(-3 ))e ^(-1 )= 0 .5 xx 10 ^(-6 ) $e^{- 1}$ ऐम्पियर नियम से
$B \times 2 π r_{1} = μ_{0} (I_{c} + I_{d})$ जहा $r_{1} =$ लूप की त्रिज्या )
$B = \frac{μ_{0}}{2 π r_{1}} (I_{c} + I_{d}) (∵ I_{c} = 0)$
$B = \frac{4 π \times 10^{- 7}}{2 π \times \frac{1}{2}} = (0 + 0.5 \times 10^{- 6} e^{- 1})$
$B = \frac{4 \times 10^{- 7} \times 0.5 \times 10^{- 6}}{e} = \frac{2 \times 10^{- 13}}{2.7}$
$B = 0.74 \times 10^{- 13}$ टेसला

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROMAGNETIC WAVES

Topper's Solved these Questions

Similar Questions

SCIENCE PUBLICATION-विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी -विविध उदाहरण

Home
Ask Doubt
Profile