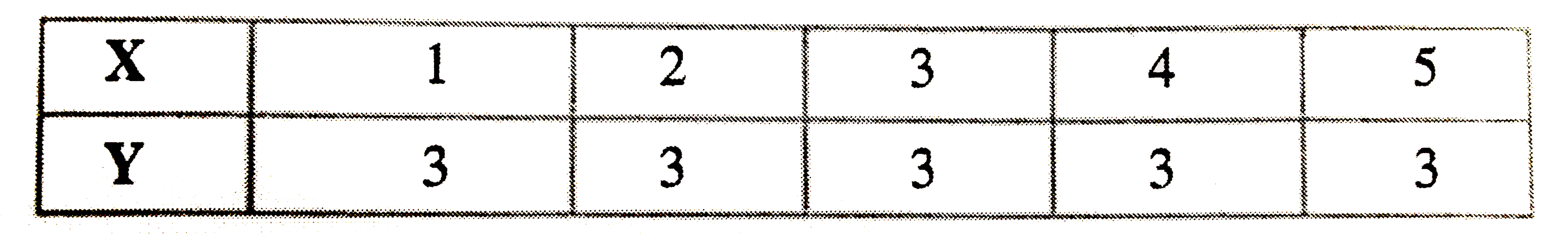Calculate the correlation cofficient beteen X and Y and comment on their relationship .

Video Solution
Text Solution

r=∑dxdy−(∑dx)×(∑dy)N√∑dx2−(∑dx)2N×√∑sy2−(∑dy)2N
r=68−(−2)×(−4)6√34−(−2)26×√136×(−4)26
68−86√34−46×√136−166
=408−86√204−46×√816−166
=4006√2006×√8006
400616√200×800
4006×61×1√1,60,000
400400=1
Correlation coefficient (r)=1
This is a situation of a perfectly positive correlation between X and Y.
|
Topper's Solved these Questions
- CORRELATIONBOOK - TARUN JAIN & VK OHRICHAPTER - CORRELATIONEXERCISE - Essential practicals
20 Videos
- CONCEPT OF ECONOMICS AND SIGNIFICANCE OF STATISTICS IN ECONOMICSBOOK - TARUN JAIN & VK OHRICHAPTER - CONCEPT OF ECONOMICS AND SIGNIFICANCE OF STATISTICS IN ECONOMICSEXERCISE - NCERT Questions
6 Videos
- DIAGRAMMATIC PRESENTATION OF DATA BAR DIAGRAMS AND PIE DIAGRAMSBOOK - TARUN JAIN & VK OHRICHAPTER - DIAGRAMMATIC PRESENTATION OF DATA BAR DIAGRAMS AND PIE DIAGRAMSEXERCISE - NCERT Question (With Hints to Answers)
3 Videos
Similar Questions
Knowledge Check
The correlation between X and a−X is
A−1B−12C−14D0If the regression coefficient of Yon X is-6 and the correlation coefficient between X and Y is -1/2. then the regression coefficient od X on Y would be
A1/24B−1/24C−1/6D1/6Let the correlation coefficient between X and Y be 0.6. Random variables Z and W are defined as Z=X+5andW=Y3. What is the correlation coefficient between Z and W?
A0.1B0.2C0.36D0.6
Calculate the correlation cofficient between the heights of Fathers in inches (X) and their sons (Y).

View SolutionCalculate rank correlation coefficient of Example 1 in Section 11.4.
View SolutionCalculate coefficient of correlation between series X and Y.

View SolutionLet the correlation coefficient between X and Y be 0.6, random variable Z and W are defined as Z=X+5 and W=y3 What is the correlation coefficient between Z and W
View SolutionIf the regression coefficient of Y on X is −6, and the correlation coefficient between X and Y −12, then the regression coefficient of X on Y would be
View Solution