An ordinary cubical dice having six faces marked with alphabets A, B, C, D, E, and F is thrown n times and the list of n alphabets showing up are noted. Find the total number of ways in which among the alphabets A, B, C D, E and F only three of them appear in the list.
Step by step video & image solution for An ordinary cubical dice having six faces marked with alphabets A, B, C, D, E, and F is thrown n times and the list of n alphabets showing up are noted. Find the total number of ways in which among the alphabets A, B, C D, E and F only three of them appear in the list. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
An ordinary cubical dice having six faces marked with alphabets A, B, C, D, E, and F is thrown n times and the list of n alphabets showing up are noted. Find the total number of ways in which among the alphabets A, B, C D, E and F only three of them appear in the list.
View SolutionAn unbiased dice, with faces numbered 1, 2, 3, 4, 5, 6, is thrown n times and the list of n numbers shown up is noted. Then find the probability that among the numbers 1, 2, 3, 4, 5, 6 only three numbers appear in this list and each number appears at least once.
View Solution
Knowledge Check
- Question 1 - Select One
Choose the right option in which all the alphabets A, B, C, D and E are correctly identified
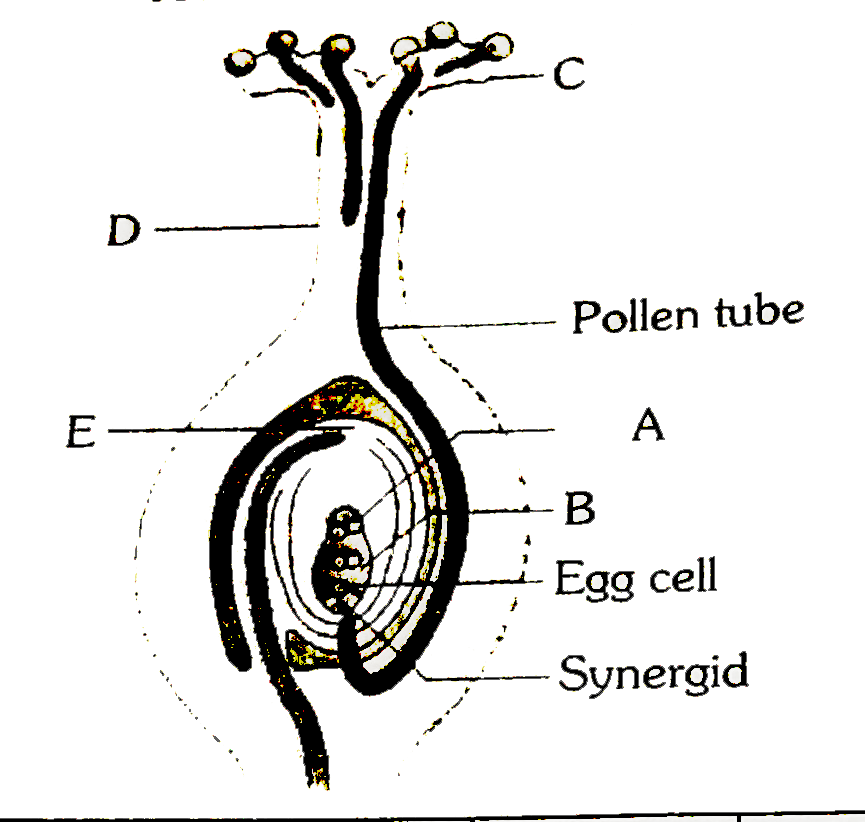 A A B C D E Antipodal cells Secondary nuclei Chalaza Stigma StyleB A B C D E Antipodal cells Secondary nuclei Stigma Chalaza StyleC A B C D E Antipodal cells Secondary nuclei Style Stigma ChalazaD A B C D E Antipodal cells Secondary nuclei Stigma Style Chalaza
A A B C D E Antipodal cells Secondary nuclei Chalaza Stigma StyleB A B C D E Antipodal cells Secondary nuclei Stigma Chalaza StyleC A B C D E Antipodal cells Secondary nuclei Style Stigma ChalazaD A B C D E Antipodal cells Secondary nuclei Stigma Style Chalaza - Question 2 - Select One
The six faces of a dice have been marked with the letters A, B, C, D, E and F. If A is adjacent to B, C and E, then which of the following statements is true?
AA is adjacent to D .BA is adjacent to FCB is adjacent to F .DD is adjacent to F . - Question 3 - Select One or More
Consider a,b,c,d,e,f,g,h to be eight distinct alphabets then the number of ways in which they can be dividied in 4- parts is
A1260 if exactly 2-parts are equalB1701in totalC280 if its divided intotwo paritions of 3 and two of 1D210 if all parts are equal
An unbiased dike, with faces numbered 1,2,3,4,5,6, is thrown n times and the list of n numbers shown up is noted. Then find the probability that among the numbers 1,2,3,4,5,6 only three numbers appear in this list.
View SolutionA,A,B,B,C,C,D,E,F are arranged in a row so that no two alike alphabets are together. Find number of such arrangment
View SolutionSix faces of the dice are A, B, C, D. E and F. A is adjacent to B. B is adjacent to D but not C. E is adjacent to D and F. What is the side opposite to A?
View SolutionSix friends A, B, C, D, E and F are sitting in a row facing East. C is between A and E. B is just to the right of E but left of D. F is not at the right end. Who is to the left of A ?
View SolutionThere are six persons A, B, C, D, E and F. C is the sister of F. B is the brother of E's husband. D is the father of A and grandfather of F. There are two fathers, three brothers and a mother in the group.
Who is the mother?View Solution

