If the above radial probaility curve indicates '2s' orbital, the distance between the peak points X& Y
is

2.07Ã…

1.59Ã…

0.53Ã…

2.12Ã…

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The maximum radial probability in $1 s$ -orbital occures at a distance when : $[r_{0} = Bohr radius]$
A $r = r_{0}$
B $r = 2 r_{0}$
C $r = \frac{r_{0}}{2}$
D $2 r = \frac{r_{0}}{2}$
The shortest distance between the lines $y - x = 1$ and the curve $x = y^{2}$ is
A $\frac{\sqrt{3}}{4}$
B $\frac{3 \sqrt{2}}{8}$
C $\frac{2 \sqrt{3}}{8}$
D $\frac{3 \sqrt{2}}{5}$
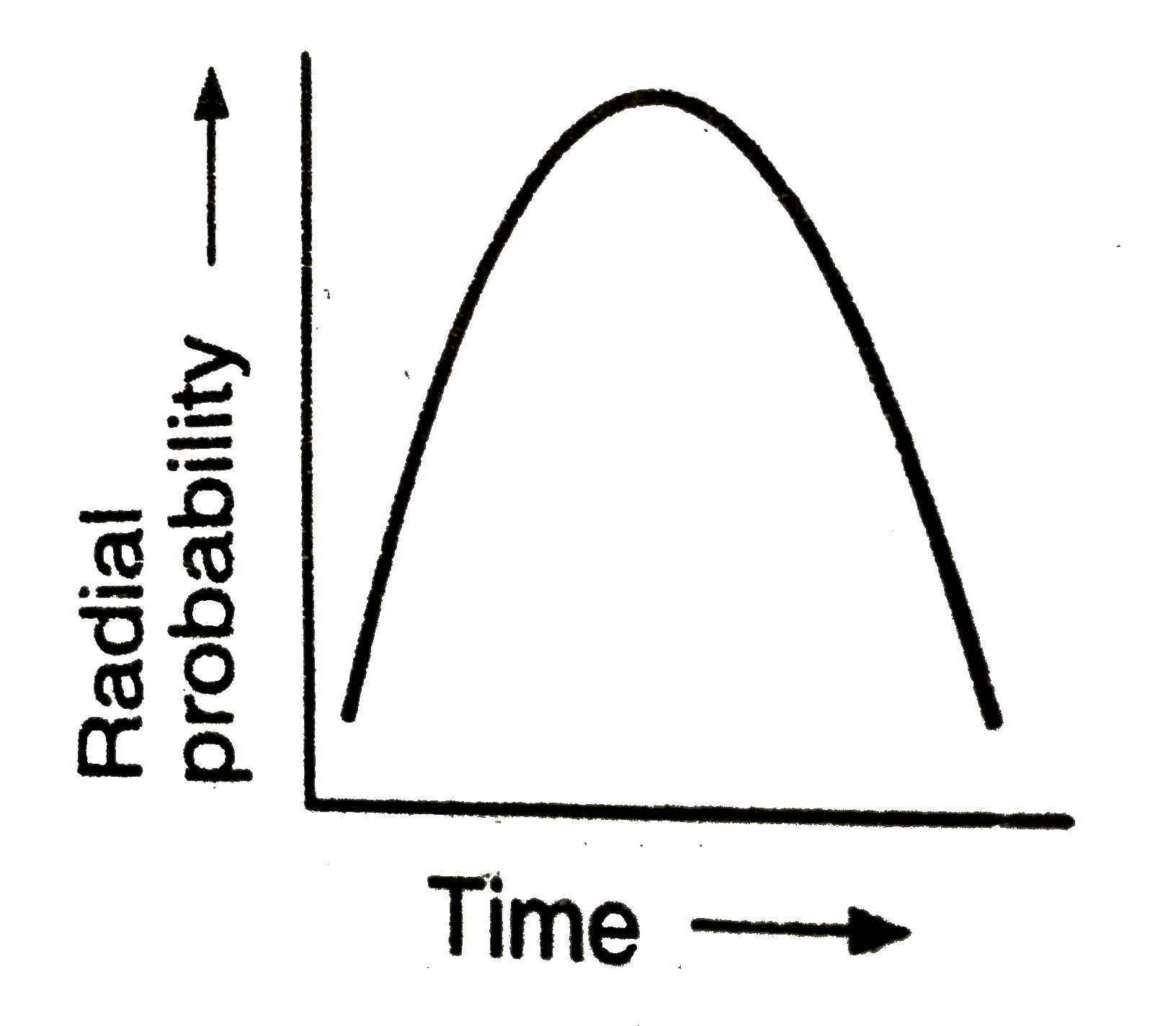
Radial probability distribution curve is shown for s-orbital. The curve is:
A1s
B2s
C3s
D4s