According to the Bohr model, the energy levels of hydrogen atom can be found by making two assumptions.
(i). The electrons move in circulr orbit and (ii) the angular momentum of the electron in the nth energy level is quantized to have a value nh2π. The levels calculated with nuclear charge Ze, with a single electron in the orbit, are called Hydrogenic levels. Assume that the two electrons in the ground state of a helium atom occupy the corresponding lowest Hydrogenic level.
Q. The minimum repulsive energy between the two electrons would then be:
A
3.4 eV
B
6.8 eV
C
13.6 eV
D
27.2 eV
Text Solution
The correct Answer is:D
For singly ionised He atom, ground state energy is
(−Ze22r)=−54.4eV
−2e22r=−54.4eV
e22r=27.2eV
∴ Minimum repulsive energy =27.2eV
(Two electrons will lie diametrically opposite).
|
Topper's Solved these Questions
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Self Assement
20 Videos
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Integer Answer Type Questions
6 Videos
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Integer Type Question
17 Videos
- AROMATIC HYDROCARBONS (ARENES)BOOK - OP TANDONCHAPTER - AROMATIC HYDROCARBONS (ARENES)EXERCISE - EXAMPLES
24 Videos
- CHARACTERISATION OF ORGANIC COMPOUNDS BOOK - OP TANDONCHAPTER - CHARACTERISATION OF ORGANIC COMPOUNDS EXERCISE - Passage-2
5 Videos
Similar Questions
Knowledge Check
According to the Bohr model, the energy levels of hydrogen atom can be found by making two assumptions.
(i). The electrons move in circulr orbit and (ii) the angular momentum of the electron in the nth energy level is quantized to have a value nh2π. The levels calculated with nuclear charge Ze, with a single electron in the orbit, are called Hydrogenic levels. Assume that the two electrons in the ground state of a helium atom occupy the corresponding lowest Hydrogenic level.
Q. if the hydrogen atom ionizatioin temperature is T, the temperature at which He atoms ionise completely (both electron having left the atom) would be:A8TB4TC6TD2TAccording to the Bohr model, the energy levels of a hydrogen atom can be found by making two assumptions.
(i) The electrons move in a circular orbit and
(ii) The angular momentum of the electron in the nth th energy level is quantised to have a value, nh2π The levels calculated with a nuclear charge Ze deals with a single electron in the orbit are called hydrogenic levels. Assume that the two electrons in the ground state of a helium atom occupy the corresponding lowest hydrogenic level.
Now match Column I with Column II and select the correct option from the choices given below the column.
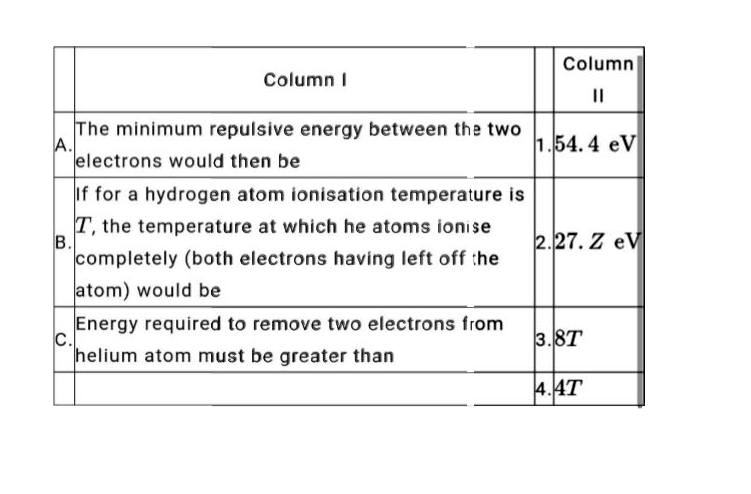 A(A) 2, (B) 4, (C) 1B(A) 1, (B) 4, (C) 3C(A) 1, (B) 3, (C) 2D(A) 2, (B) 3, (C) 1
A(A) 2, (B) 4, (C) 1B(A) 1, (B) 4, (C) 3C(A) 1, (B) 3, (C) 2D(A) 2, (B) 3, (C) 1In the lowest energy level of hydrogen atom, the electron has the angular momentum
Aπ/hBh/πCh/2πD2π/h
The speed of the electron in a hydrogen atom in the n = 3 level is
View SolutionThe angular speed of the electron in the nth Bohr orbit of the hydrogen atom is proportional to
View SolutionThe angular speed of the electron in the nth Bohr orbit of the hydrogen atom is proportional to
View SolutionThe energy of an electron in nth orbit of hydrogen atom is
View SolutionIn Bohr's orbit, kinetic energy of an electron in the nth orbit of an atom in terms of angular momentum is
View Solution
