If a<b<c<d & x ∈R then the least value of the function, f(x)=|x−a|+|x−b|+|x−c|+|x−d| i s c−d+b−a (b) c+d−b−a c+d−b+a (d) c−d+b+a
Step by step video & image solution for If a<b<c<d\ &\ x\ in R then the least value of the function, f(x)=|x-a|+|x-b|+|x-c|+|x-d|\ "i s" c-d+b-a (b) c+d-b-a c+d-b+a (d) c-d+b+a by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Evaluate the following limits ([.], {.} denotes greatest integer function and fractional part respectively) (lim)x→n[x], (lim)x→n{x}, n∈I
View SolutionIf cosxa=cos(x+θ)b=cos(x+20)c=cos(x+3θ)d then a+cb+d is equal to (a)ad (b) cb (c) bc (d) da
View Solutiona<b<c<d&x∈R then the least value of the function, f(x)=|x−a|+|x−b|+|x−c|+|x−d| is
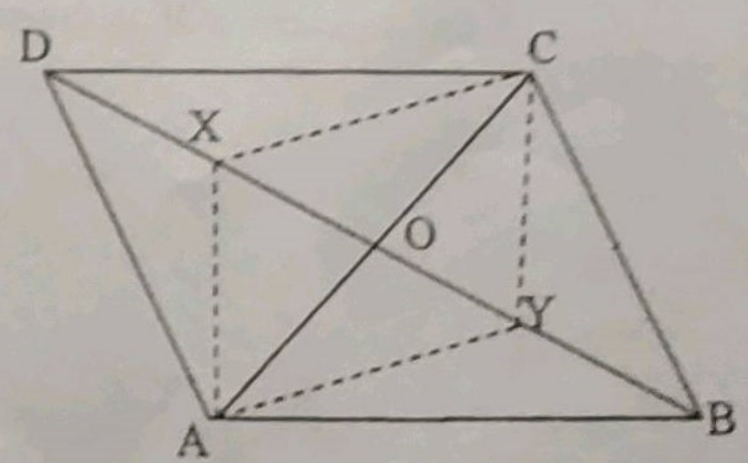
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View Solutionif x=a−ba+b+c+d=b−ca+b+c+d=c−da+b+c+d
=d−aa+b+c+d, then find x3.
View Solution(x−a)(x−b)(x−c)(x−d)=Ax−c−Bx−d+C⇒C=
View Solution((x-a)(x-b))/((x-c) (x-d)) = (A)/(x-c) - (B)/((x-d)) +C , Then C =
View SolutionIf cosxa=cos(x+θ)b=cos(x+20)c=cos(x+3θ)d then a+cb+d is equal to (a)ad (b) cb (c) bc (d) da
View SolutionIf cosxa=cos(x+θ)b=cos(x+2θ)c=cos(x+3θ)d then a+cb+d is equal to (A)ad(B)cd(C)bc(D)da
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View SolutionIf a+bexa−bex=b+cexb−cex=c+dexc−dex then a, b, c, d are in
View SolutionIf a3(x−b)(x−c)(x−d)(a−b)(a−c)(a−d)+b3(x−c)(x−d)(x−a)(b−c)(b−d)(b−a)+c3(x−d)(x−a)(x−b)(c−d)(c−a)(c−b)+d3(x−a)(x−b)(x−c)(d−a)(b−d)(d−c)=x^3,then the equation having
View SolutionIf a+bxa−bx=b+cxb−cx=c+dxc−dx(x≠0), then show that a,b,c and d are in G.P.
View SolutionIf a⟨b⟨c⟨d and x∈R then the least value of the function, f(x)=|x−a|+|x−b|+|x−c|+|x−d| is
View SolutionIf cosxa=cos(x+θ)b=cos(x+20)c=cos(x+3θ)d then a+cb+d is equal to (a)ad (b) cb (c) bc (d) da
View Solution
