Assertion: The given equation x=x0+u0t+12at2 is dimensionsally correct, where x is the distance travelled by a particle in time t , initial position x0 initial velocity u0 and uniform acceleration a is along the direction of motion.
Reason: Dimensional analysis can be used for cheking the dimensional consistency or homogenetly of the equation.
if both assertion and reason are true reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation fo assertion.
If assertion is true but reaso is false.
IF both assertion and reason are false.
The correct Answer is:A
Given equation x=x0+u0t+12at2.
The dimensions of each term may be written as
[x]=[L],[x0]=[L],[u0t]=[LT−1][T]=[L]
[(12)at2]=[LT−2][T2]=[L]
As each ter on the right hand side of this equation has the same dimension as left hand side of the equation, hence this equation is dimensionally correct.
Topper's Solved these Questions
Similar Questions
Check the accuracy of the relation s=ut+12at2 where s is the distance travelled by the with uniform acceleration a in time t and having initial velocity u.
View SolutionFigure gives the x-t plot of a particle is one dimensional motion. Give the signs of position, velocity and acceleration of the particle at t = 0.3s
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The x-t curve shown in the figure provides following position
x0 = Initial position
v0 = initial velocity , a = acceleration
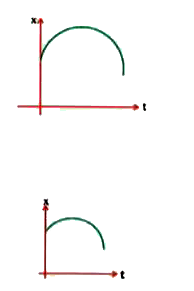 Ax0≠0,v0>0, a is -iveBx0≠0,v0>0, a is +iveCx0≠0,v0<0, a is +iveDx0≠0,v0<0, a is -ive
Ax0≠0,v0>0, a is -iveBx0≠0,v0>0, a is +iveCx0≠0,v0<0, a is +iveDx0≠0,v0<0, a is -ive - Question 2 - Select One
The initial velocity of a particle is u (at t=0) and the acceleration f is given by at. Which of the relation is valid
Av=u+at2Bv=u+at22Cv=u+atDv=u - Question 3 - Select One
The distance x covered in time t by a body having initial velocity v0 and havig a constant acceleration a is given by x=v0t+(12)at2. This result follows from:-
ANewton's first lawBNewton's second lawCNewton's third lawDNone of the above
The displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionThe distance x covered in time t by a body having initial velocity v0 and havig a constant acceleration a is given by x=v0t+(12)at2. This result follows from:-
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe initial velocity of a particle is u (at t = 0) and the acceleration f is given by f = at. Which of the following relation is valid?
View Solution

