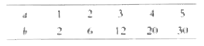
The relation between Y. η and B is
1Y=13η+19B
9Y=1η+3B
1η=1B+1Y
9Y=3η+1B
The correct Answer is:D
To find the relation between Young's modulus (Y), modulus of rigidity (η), and bulk modulus (B), we can follow these steps:
Step 1: Understand the Definitions
- Young's Modulus (Y): It measures the tensile or compressive stiffness of a solid material.
- Modulus of Rigidity (η): It measures the material's response to shear stress.
- Bulk Modulus (B): It measures a material's response to uniform pressure applied in all directions.
Step 2: Write the Relationships
From the video transcript, we have two important relationships:
1. Y=2η(1−μ)
2. B=Y3(1−2μ)
Where μ is the Poisson's ratio.
Step 3: Rearranging the Equations
From the first equation, we can express η:
η=Y2(1−μ)
From the second equation, we can express Y in terms of B:
Y=3B(1−2μ)
Step 4: Substitute and Rearrange
Now, substituting the expression for Y from the second equation into the first equation:
η=3B(1−2μ)2(1−μ)
Step 5: Finding the Relation
To find a relation between Y, η, and B, we can manipulate these equations further.
Using the relationships derived:
1. Y=2η(1−μ)
2. Y=3B(1−2μ)
We can equate the two expressions for Y:
2η(1−μ)=3B(1−2μ)
Step 6: Final Relation
This can be rearranged to find a relation involving Y, η, and B:
9Y=3η+1B
Thus, the final relation between Young's modulus (Y), modulus of rigidity (η), and bulk modulus (B) is:
9Y=3η+1B
Conclusion
The correct answer is option 4, which states the derived relation.
---
- Young's Modulus (Y): It measures the tensile or compressive stiffness of a solid material.
- Modulus of Rigidity (η): It measures the material's response to shear stress.
- Bulk Modulus (B): It measures a material's response to uniform pressure applied in all directions.
From the video transcript, we have two important relationships:
1. Y=2η(1−μ)
2. B=Y3(1−2μ)
From the first equation, we can express η:
η=Y2(1−μ)
Y=3B(1−2μ)
Now, substituting the expression for Y from the second equation into the first equation:
η=3B(1−2μ)2(1−μ)
To find a relation between Y, η, and B, we can manipulate these equations further.
1. Y=2η(1−μ)
2. Y=3B(1−2μ)
2η(1−μ)=3B(1−2μ)
This can be rearranged to find a relation involving Y, η, and B:
9Y=3η+1B
9Y=3η+1B
The correct answer is option 4, which states the derived relation.
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Applications Of Elastic Behaviour Of Materials8videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Higher Order Thinking Skills8videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Stress-Strain Curve5videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason15videos
MOTION IN A PLANE
Similar Questions
Knowledge Check
- Question 1 - Select One
If x16=y23, then relation between x and y is
Ax=y2Bx=y4Cx4=yDx3=y8 - Question 2 - Select One
The relation betweent γ,η and K for a elastic material is
A1η=13γ+13KB1K=13γ+19ηC1γ=13K+19ηD1γ=13η+19K - Question 3 - Select One
Relation between Y,ηandKis
AY3=3K+1ηB9Y=η3+1KC3Y=1η+13KDY3=3η+1K
The relation between BH,Bv,andB is
View SolutionIf x% of y is 150 and y% of z is 300, then the relation between x and z is :
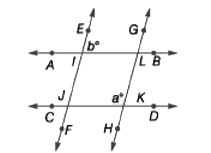
यदि y का x% 150 है और z का y% 300 है, तो x और z में क्या संबंध है ?View SolutionIn the given figure, AB \\ CD and EF // GH. Find the relation between a and b.
 View Solution
View SolutionRelation between (A) and (B) is :
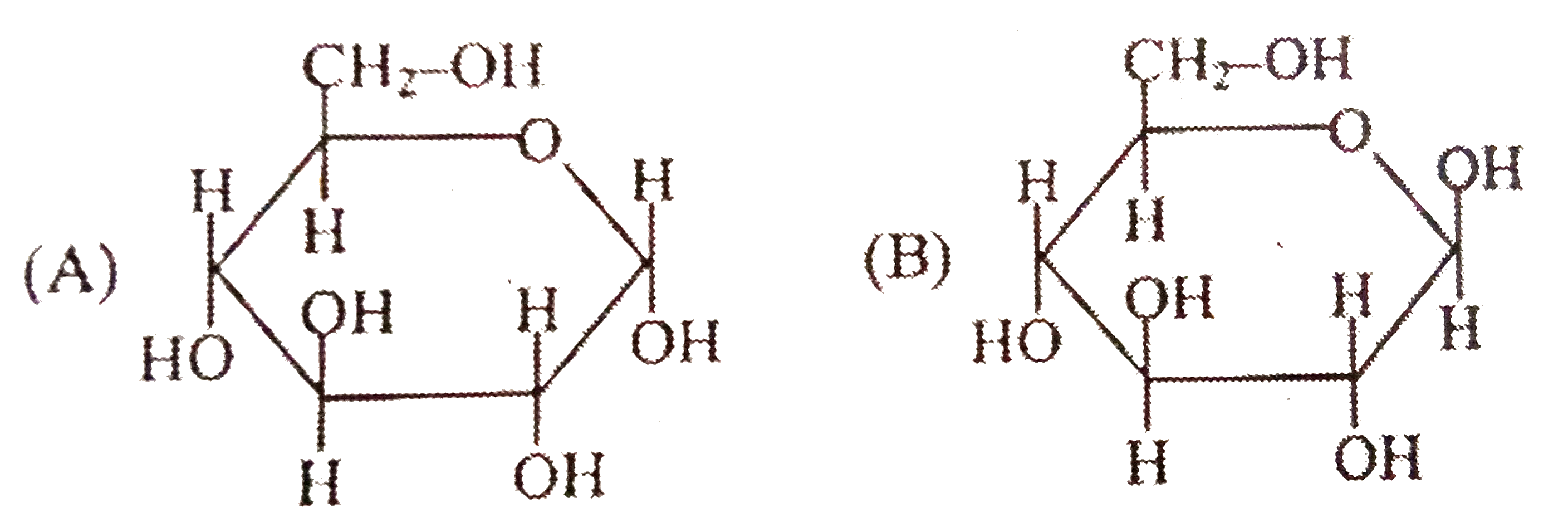 View Solution
View SolutionExpress the relation between a and b with b as the subject.
 View Solution
View Solution