The radii of the two columne is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
ρghr1r22(r2−r1)
ρgh(r1−r2)2r1r2
2(r2−r1)ρghr1r2
ρgh2(r2−r1)
The correct Answer is:A
Let h1,h2 be the heights to which liquid rises in two columns of radii r1 and r2 respectively. Then
h1=2ScosO∘r1ρg=2Sr1ρg
Where s is the surface tension of liquid.
and h2=2Scoso∘r2ρg=2Sr2ρg
∴ Difference in levels of liquid in two arms of U tube is
h=h1−h2=2Sρg[1r2−1r2]=2S(r2−r1)r1r2ρg
S=r1r2ρgh2(r2−r1)
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Higher Order Thinking Skills8videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Reynolds Number4videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason15videos
LAWS OF MOTION
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
The radii of two columns in a U tube are r1andr2(r1>r2). A liquid of density ρ is filled in it. The contact angle of the liquid with the tube wall is θ. If the surface tension of the liquid is T then plot the graph of the level difference (h) of the liquid in the two arms versus contact angle θ. Plot the graph for angle θ changing from 0∘→90∘. Assume the curved surface of meniscus to be part of a sphere.
 View Solution
View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -
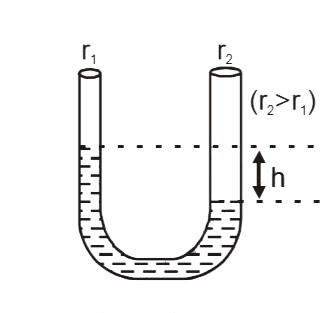 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
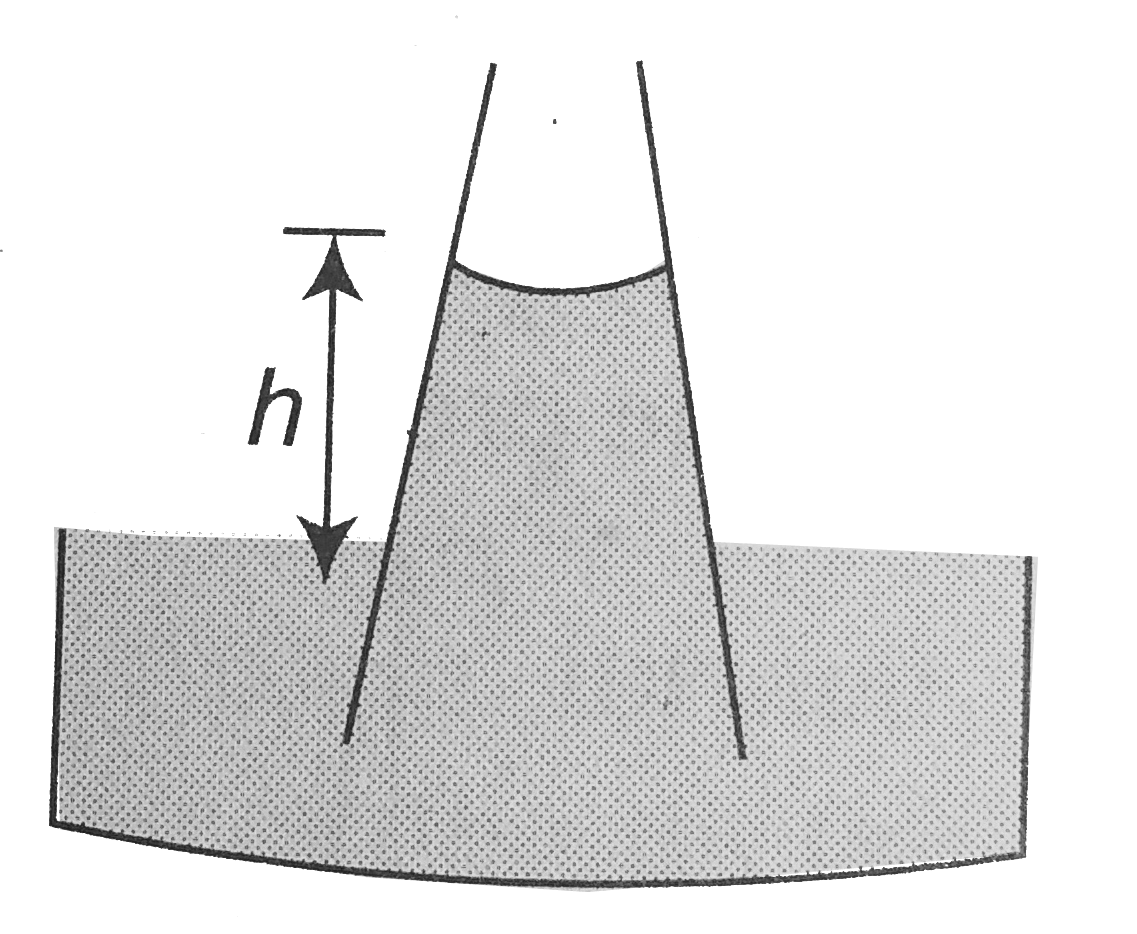
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:Agreater than 2TrρgBequal to 2TrρgCless than 2TrρgDof any value depending upon act. - Question 2 - Select One
A beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
AhρgBhρ(g+a)Chρ(g−a)D2hρg(g−ag+a) - Question 3 - Select One
If h is the rise of water in a capillary tube of radius r, then the work done by the force of surface tension is
(ρ is density g = (acc)n due to gravity )A2gT2ρπB2πT2ρgC4gT2ρπD4πT2ρg
A container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
View SolutionStatement-1: The angle of contact of a liquid decrease with increase in temeperature
Statement-2: With increase in temperature the surface tension of liquid increase.View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
What is the potential energy acquired by the liquid in the capillary?View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

If density of lower liquid is increasedView SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View Solution

